
相関分析をわかりやすく解説!基本、エクセルのやり方、事例
目次[非表示]
- ・ はじめに
- ・相関分析とは
- ・相関関係と因果関係の違い
- ・相関分析と回帰分析の違い
- ・相関係数
- ・相関分析の活用シーン
- ・相関分析の流れ、やり方
- ・相関分析にまつわる、よくある質問
- ・ Q:相関分析では「外れ値」の影響を考慮しなければならないと聞きますが、「外れ値」は必ず除外したほうが良いのでしょうか。
- ・ Q:相関分析の流れとして、必ず散布図を先に作成してから、相関係数を算出しなければならないのでしょうか。
- ・ Q:散布図の近似曲線の「R2乗値」は、相関係数とは異なるのでしょうか。
- ・ Q:相関係数は、Excelの「CORREL関数」で簡単に算出できますが、なぜ操作に手間のかかるExcelの「データ分析ツール」を使わなければならないのでしょうか。
- ・ Q:「見せかけの相関」とは何でしょうか。具体的にどのような例がありますか。
- ・ 無料ダウンロード『相関分析マニュアル~Excelを使ったわかりやすい分析の手順~』
- ・おわりに(まとめ)
はじめに
ここでは相関分析について、基本的な知識をはじめ、分析の流れ、エクセルを使った手順・やり方を、図解と事例を交えながら、分かりやすく解説していきます。
この記事を読んで分かること、できるようになること
●相関分析の意味、基本知識、因果関係や回帰分析との違いが理解できる。
●相関分析のやり方を理解し、Excelを使って実行できるようになる。
●相関分析に関するQ&Aやまとめ資料を、無料でダウンロードできる。
相関分析とは
相関分析とは、2つの変数の相互関係を分析することです。
具体的には、例えばXとYという2つの変数がある場合、変数Xの値が大きくなるにつれ、変数Yの値も大きくなれば正の相関があると言います。逆に、変数Xの値が大きくなるにつれ、変数Yの値が小さくなれば負の相関があると言います。
そのどちらでもない場合、XとYの間には相関はないと言います。
相関関係と因果関係の違い
勘違いしてしまうことが多いのですが、相関関係は因果関係とは異なります。
相関関係とは、「鶏が先か卵が先か」のように2つの変数のうち、どちらが原因でどちらが結果かわからないが、とにかく相互に関係し合っていることです。
これに対して因果関係とは、一方が原因で他方が結果の関係です。
まとめると、相関関係はX⇔Yという双方向の関係、因果関係はX⇒Yという一方向の関係となります。
相関分析と回帰分析の違い
回帰分析とは、XとYという2つの変数に明らかな因果関係がある、と認められる場合に、その変数同士の関係を分析することです。Xに対してYがどのような影響を及ぼしているかを突き止めます。
相関分析とは異なり、Xの値をもとにしてYの値を算出します。数式はY=aX+bとなります。
その変数が2つの場合を「単回帰分析」、変数が3つ以上の場合を「重回帰分析」と言います。
相関係数
相関係数とは
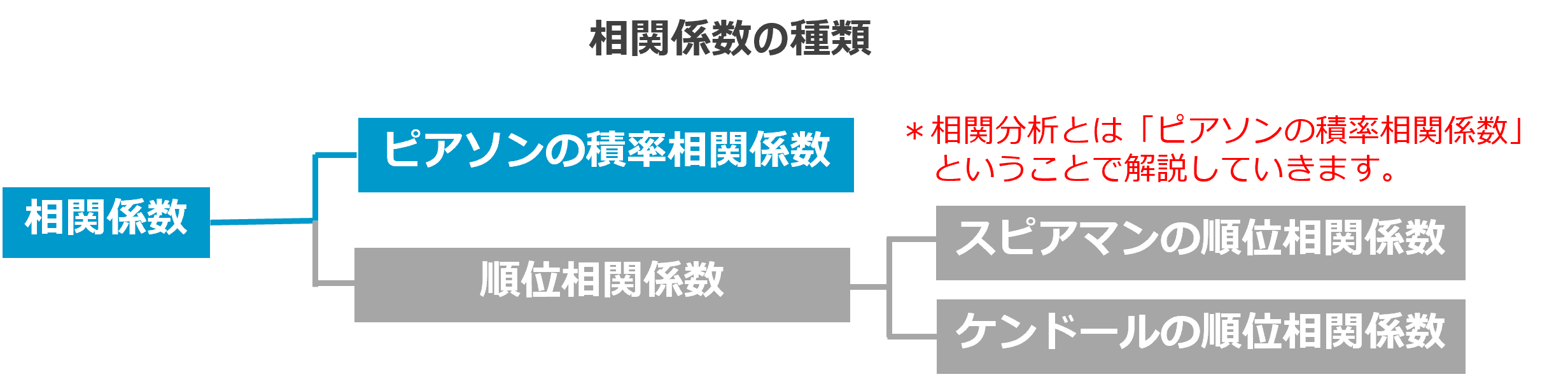
相関係数とは、2つの独立した変数の相関が強いか弱いか(相関関係の強さ)を示す数値のことです。相関係数には大きく二つの種類があります。
ピアソンの積率相関係数
一般的に相関係数とは、「ピアソンの積率相関係数」のことを言い、以下の数式で算出できます。

なお、ピアソンの積率相関係数(一般的な相関係数)は、数式を意識することなく、Excelの関数と分析ツールで簡単に算出できます。(詳しくは後述参照)
順位相関係数
もう一つの相関係数は「順位相関係数」です。こちらは、データが順位となっている場合に使われます。
例えばプロ野球の順位予想と実際の結果の順位相関係数を算出して、高い正の相関が認められれば、「順位予想力は高い」ということになります。
※順位相関係数は、さらに「スピアマンの順位相関係数」と「ケンドールの順位相関係数」に分けられますが、ここでは詳細な解説は省きます。
相関係数値の基準
正の相関係数は「0」から「1」の間の数値となりますが、相関関係の強弱の統計的基準はありません。対象となるカテゴリーによっても異なり、都度、分析者の判断によります。
あくまでも参考ですが、以下のような基準もあります。

なお、負の場合の相関係数は「0」から「-1」の間の数値となります。
相関分析の活用シーン
相関分析は、主に2つのシーンで活用されています。
1つ目は、膨大なデータから関係性がある項目を抽出したい時です。具体的には、アンケート調査の評価項目間の相関分析は、頻繁に行われています。
生活者に身近な例としては、AmazonなどECサイトの関連商品レコメンドのアルゴリズムに使われています。
2つ目は、ある変数同士に関係性があることを客観的に示したい時です。数値化することで、個人の主観ではなく、関係性がしっかりと見え、確認することができます。
相関分析の流れ、やり方
次に相関分析の具体的なやり方を見てみましょう。『1.散布図の作成→2.近似曲線の作成→3.相関係数の算出→4.結果の検証』という4ステップで進めていきます。
1.散布図の作成
散布図作成の目的
相関分析を行う最初のステップは散布図の作成です。散布図を作成する理由は、一つ一つのデータがどのように分布しているのかを一目で俯瞰でき、データ間に相関関係があるのか無いのか、あるとすれば正の相関か負の相関かということが分かるからです。
さらに、分析結果に影響する「データの値が異常に大きい・小さい」という「外れ値」の有無も確認することができます。外れ値が発見された場合、必要によっては削除することもあります。
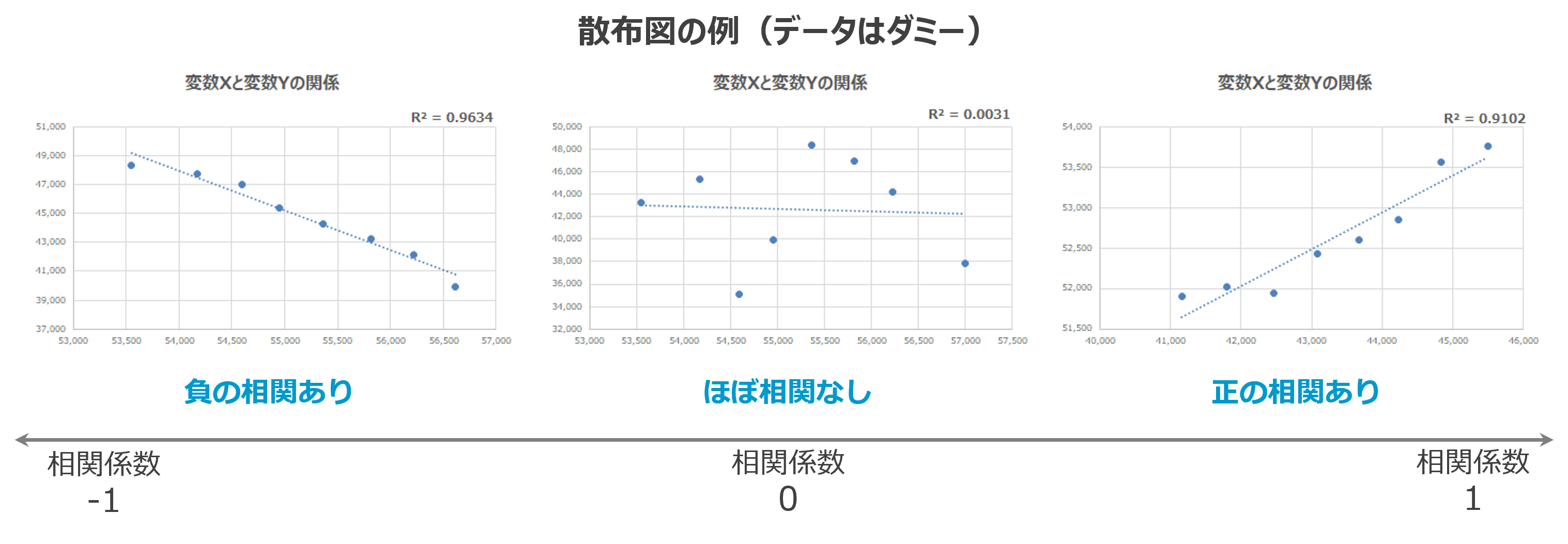
散布図の例
「負の相関あり」「ほぼ相関なし」「正の相関あり」の3パターンの散布図例が下記です。
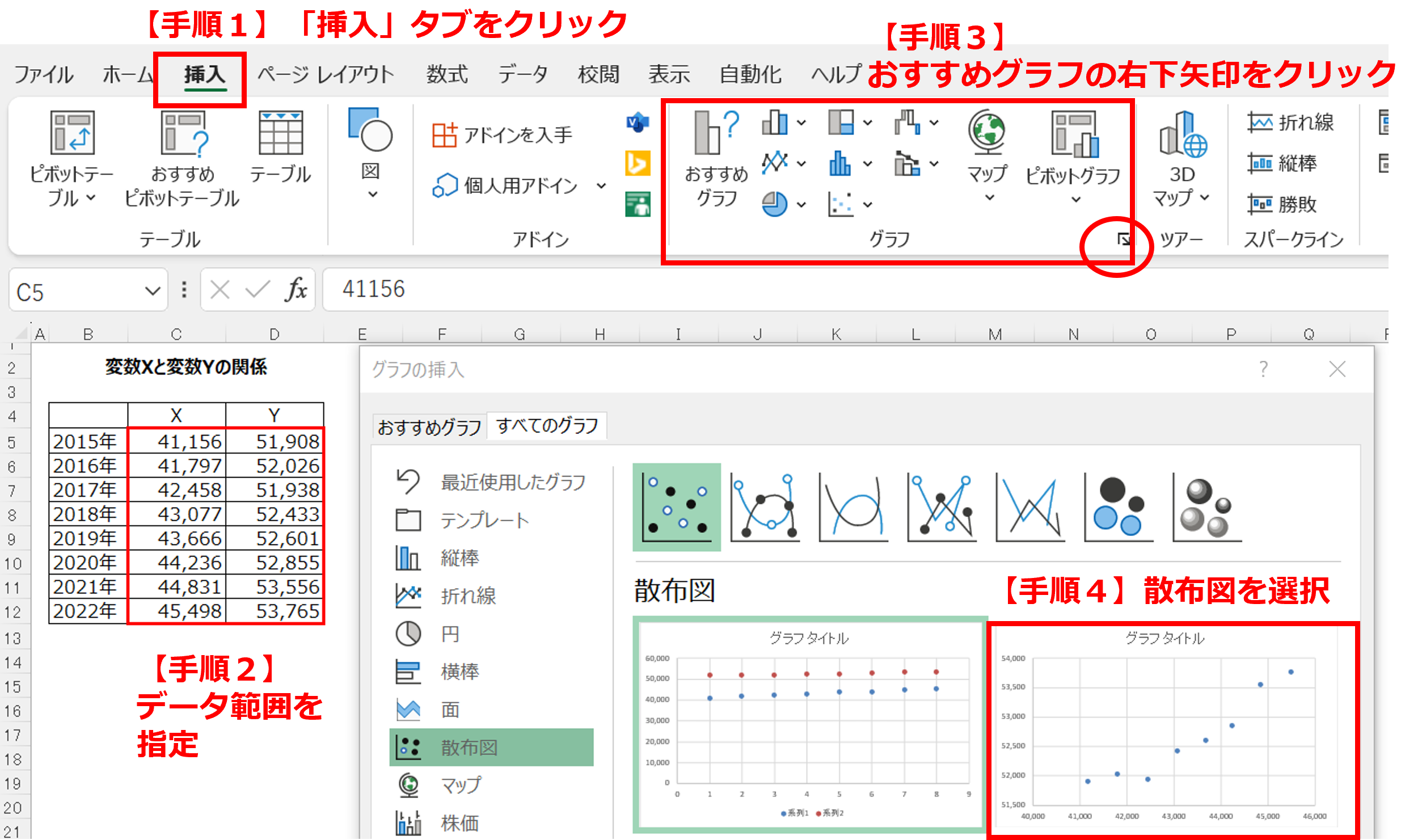
Excelによる散布図の作成方法
前項に出てきた【相関のある散布図(正の相関あり)】を例に、Excelで散布図を作成していく手順を説明します。(変数XとYは、2015年から2022年までのダミーデータです。)
|
2.近似曲線の作成
続いて、作成された散布図の一ヶ所にカーソルを合わせて右クリックすると、シート右側に「近似曲線の書式設定」が表示されるので、散布図に「近似曲線」を選択して表示させます。
|
※「R2乗値」とは、相関分析の当てはまり度合いを表す値のことで、0から1までの値をとります。「決定係数」や「寄与率」とも呼ばれ、データの並びが直線の場合に最大の「1.0」となります。
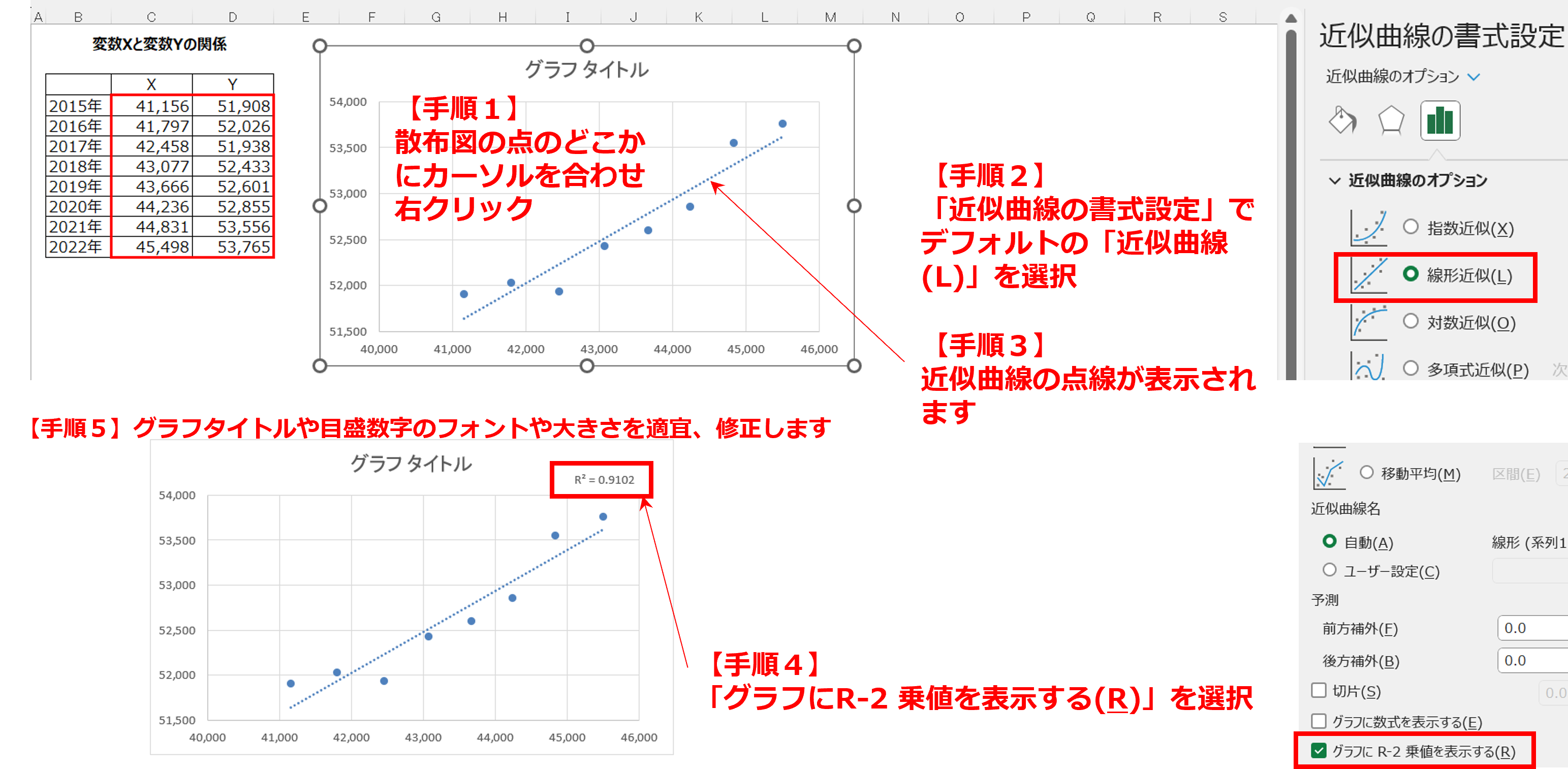
《手順4》の結果、下記のようにこのグラフの場合のR2乗値は「0.91」なので、データの並びが極めて直線に近いことがわかります。

3.相関係数の算出
次に、相関係数で、変数間に「どの程度の相関関係があるのか」を具体的な数値で把握しましょう。
Excelの「関数」を使う方法
ここでは「CORREL関数」を使用します。CORRELとは、コリレーション関数と読み、相関係数を求める関数です。
●《手順》 ExcelシートのC列の14行目に、相関係数を算出する関数「=CORREL(C5:C12,D5:D12)」と入力します。関数は「CORREL」で、()の中に変数XのC5からC12、変数YのD5からD12の範囲を指定します。 |
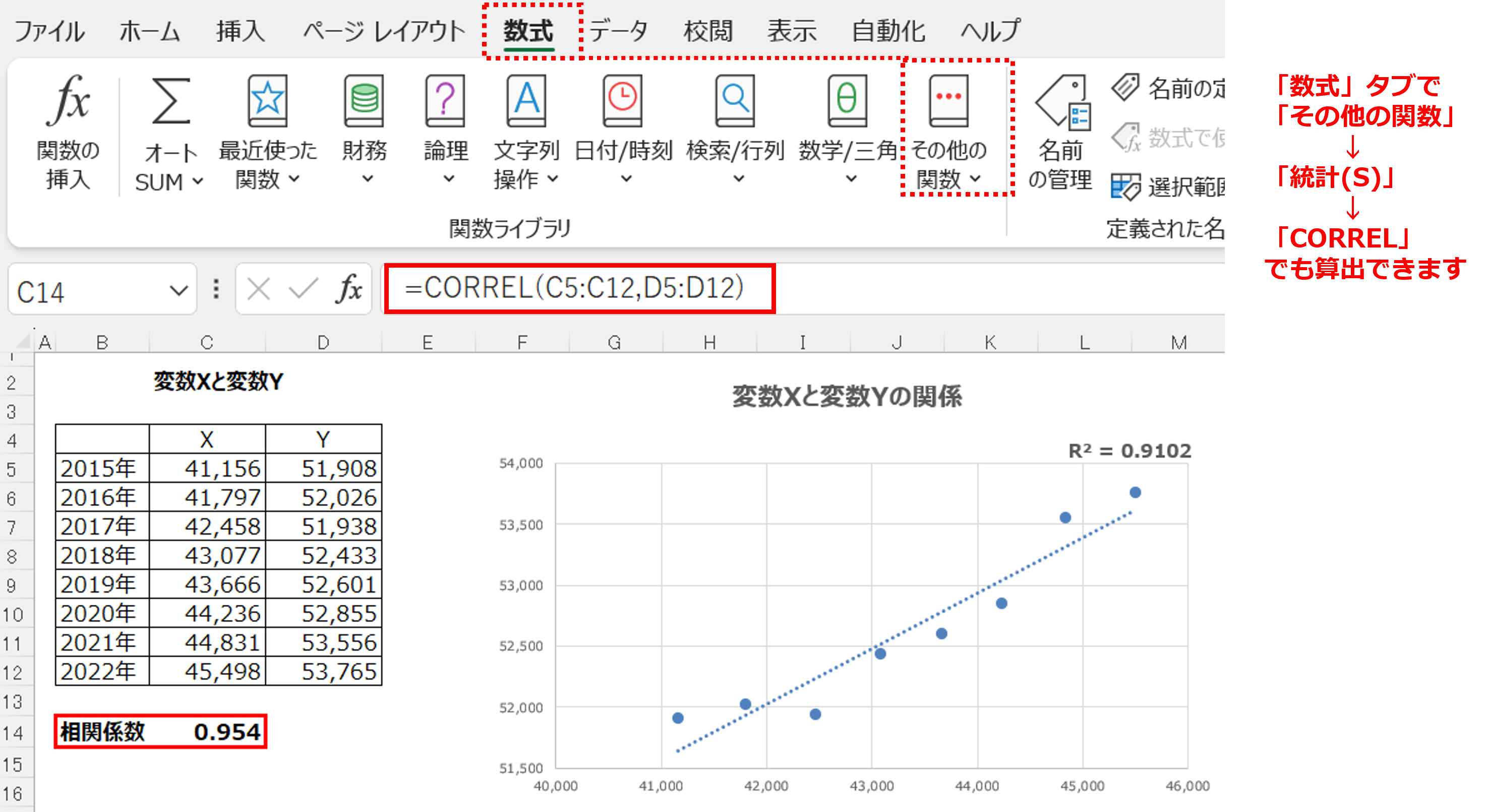
結果、相関係数は0.954でした。正の相関係数の範囲は0~1ですので、とても高いことがわかりました。
Excelの「データ分析」を使う方法
相関係数の算出は、前述のCORREL関数以外に、Excelの「データ分析」ツールを使う方法もあります。
●《手順1》「データ」タブの右側の「データ分析」をクリックすると表示されるボックスから、「相関」を選び、「OK」をクリックします。 |

●《手順2》分析ツールのボックスの「相関」の「OK」をクリックすると、「相関」のボックスが表示されるので、「入力範囲(I)」にカーソルを合わせ、数表のC5からD12を範囲指定します。 ●《手順3》相関分析の結果の「出力先(Q)」の表示先をB14とします(デフォルトは「新規ワークシート」になっており、そのまま「OK」をクリックすると、相関分析結果の数表が表示された別シートが生成されます)。 |
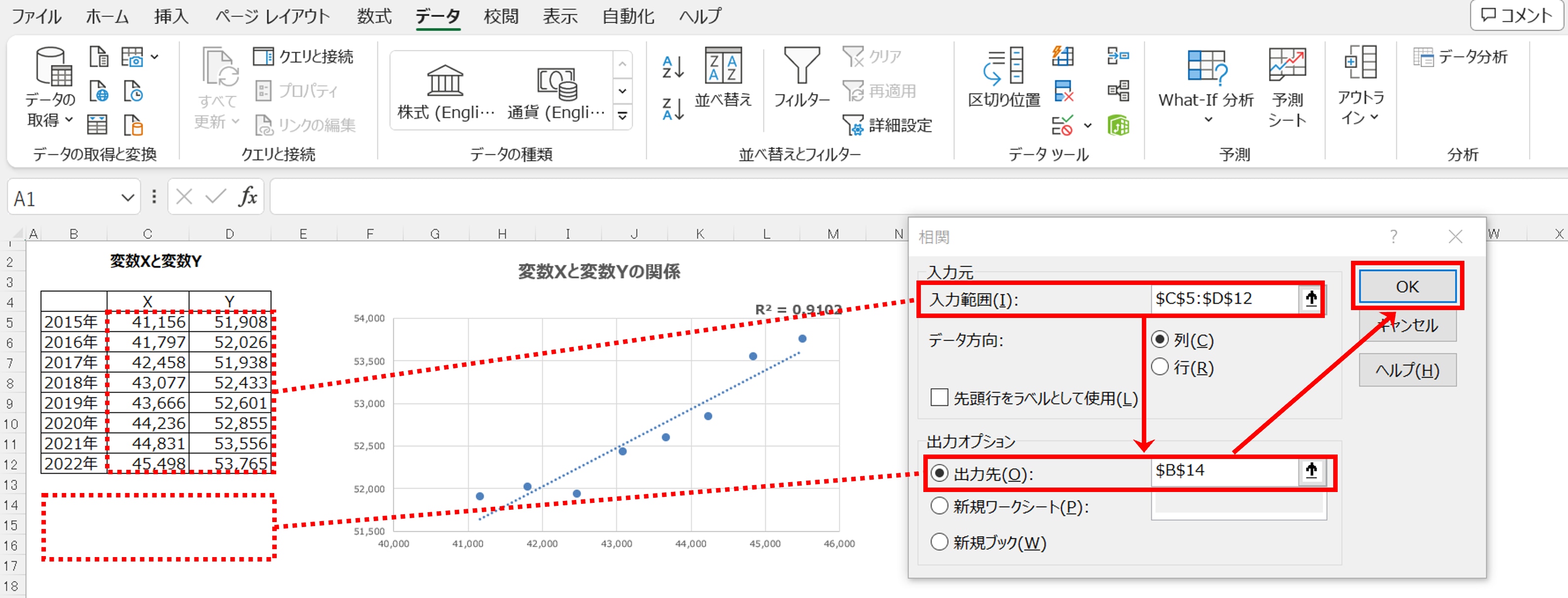
「出力先(Q)」の表示先に指定したB14のセルに、相関分析結果の行列表(B14からD16の範囲)が表示されました。
結果、相関係数は、CORREL関数で算出されたのと同じ0.954でした。
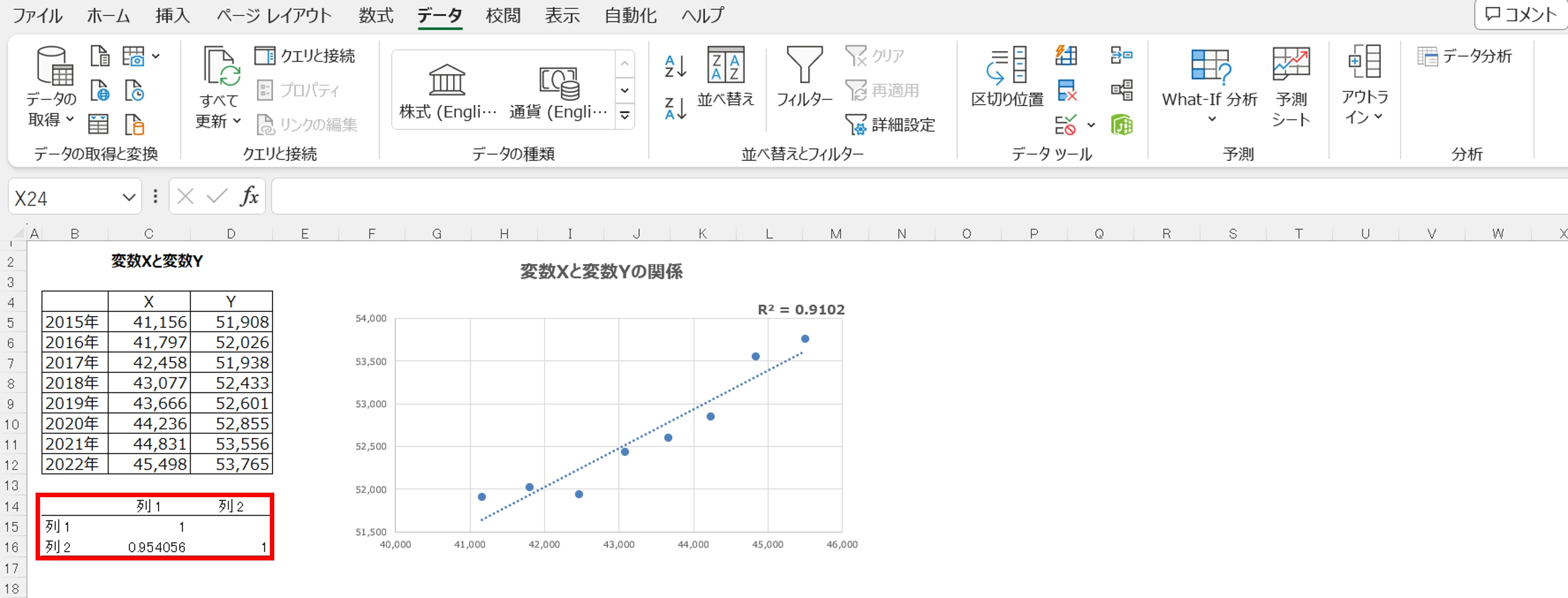
なお参考までに、Excelのデータ分析ツールは、相関分析の他にも、基本統計量や回帰分析などができる便利なツールです。別記事にて詳しいやり方を解説しているので、ご興味のある方は是非ご覧ください。
⇒分かりやすい!「アンケート集計と分析の基本|Excelを活用したまとめ方」はこちらから
相関分析にまつわる、よくある質問
Q:相関分析では「外れ値」の影響を考慮しなければならないと聞きますが、「外れ値」は必ず除外したほうが良いのでしょうか。
「外れ値」がタイプミスや不正回答であることが明白な場合は、迷うことなく除外すべきですが、全ての「外れ値」を除外すれば良いとは限りません。
「外れ値」を含めて集計すると相関係数の数値は低下しますが、どうして「外れ値」があるのかを検討することが必要な場合もあります。例えば、医薬品の効果に関するデータの「外れ値」は、それが副作用を示唆する場合もあり、除外するわけにはいきません。
データの性質、分析の目的などを考え、ケースバイケースで検討しましょう。
Q:相関分析の流れとして、必ず散布図を先に作成してから、相関係数を算出しなければならないのでしょうか。
必ずしも「散布図」を先に作成してから相関係数を算出しなければならないことはありませんが、最初に「相関係数を算出」した場合「外れ値」があったとしても見つけることは困難です。
まず最初に散布図を作成することで、データの分布が一目で俯瞰できるため、「外れ値」があった場合にすぐに見つけることができるという利点があることを覚えておきましょう。
Q:散布図の近似曲線の「R2乗値」は、相関係数とは異なるのでしょうか。
とても似ていますが、異なります。「R2乗値」は「データの並びがどれだけ直線に近いのか?」を表す値のことです。相関係数と同じく「1」が最大です。
当記事で解説している【相関分析の流れ、やり方>2.近似曲線の作成】の例に出てくる「R2乗値」は「0.91」、【相関分析の流れ、やり方>3.相関係数の算出にてExcelの「関数」を使う方法】の例に出てきた「相関係数」は『0.954』で、一見似ていますが、異なる数値でした。
Q:相関係数は、Excelの「CORREL関数」で簡単に算出できますが、なぜ操作に手間のかかるExcelの「データ分析ツール」を使わなければならないのでしょうか。
確かに「CORREL関数」で簡単に算出することができますが、それは変数が2つの場合のみです。
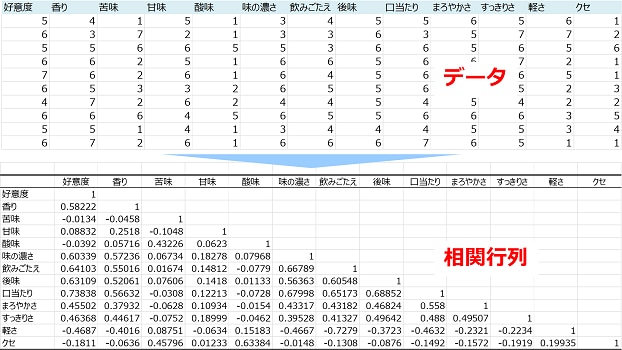
例えば以下のデータと相関行列は、ある飲料の「好意度」と「香り」から「クセ」までの「香味特性」12項目、合計13項目のデータ間の相関係数を算出した例です。
データ分析ツールであれば、このように3つ以上の変数の各々2つの変数間の相関係数を、1回の操作で算出できるため、使ったほうが便利です。
Q:「見せかけの相関」とは何でしょうか。具体的にどのような例がありますか。
「見せかけの相関」とは、「疑似相関」とも呼ばれていて、一見関係のなさそうな変数同士に関係がありそうな傾向が見出されることを言います(因果関係が無いにも関わらず、ありそうに見えること)。データマイニングを行うときに稀に起こります。
例えば、米の消費量とパソコンの出荷台数の相関係数が0.8と、とても高かったとします。しかし米の消費量が増えればパソコンの出荷台数が増えるのは、表面的な「現象」です。
実際には原因としての人口の増加が、米の消費量もパソコンの出荷台数も押し上げているわけで、米とパソコンだけの相関関係があるわけではありません。

無料ダウンロード『相関分析マニュアル~Excelを使ったわかりやすい分析の手順~』
本記事で解説した内容をまとめた資料「相関分析マニュアル~Excelを使ったわかりやすい分析の手順~」は、下記よりダウンロードすることができます(無料)。
おわりに(まとめ)
最後に、ここまで解説してきた内容をまとめました。今一度の確認に活用してください。
●相関分析とは、2つの変数の相互関係を分析することであり、その変数間には必ずしも因果関係があるわけではない
相関分析とは、2つの変数の相互関係を分析することで、一つの変数の値が大きくなるにつれ、もう一つ変数が大きくなれば「正の相関」関係にある、逆に小さくなれば「負の相関」関係にあると言います。このどちらかの関係がなければ、2つの変数の間に「相関はない」ということになります。
また、相関関係は、因果関係とは異なり、2つの変数の関係が原因でも結果でもありません(双方向)。原因と結果が明らかな場合(一方向/仮説も含め)は因果関係があるとして回帰分析を行います。
●相関分析の手順は、最初に散布図を作成してデータの分布を一目で把握してから、相関係数を算出する
最初に「外れ値」を見つけるためにも散布図を作成し、データの分布を一目で把握してから、相関係数を算出します。
相関係数は、変数の数が2つの場合、Excelの「CORREL関数」で簡単に算出することができます。変数の数が3つ以上の場合は、Excelのデータ分析ツールを使います。
●相関係数が0.8以上で「とても相関がある」
相関係数は、0.8以上で「とても相関がある」、0.5以上で「相関がある」とされています。相関の有り無しの分岐点は0.3と判断していいでしょう。負の相関の場合、数値はマイナスとなります。
【参考文献】
『ウルトラ・ビギナーのためのSPSSによる統計解析入門』(小田利勝著、プレアデス出版、2007年6月)/『Excelで学ぶ統計解析入門』(菅民郎著、オーム社、2016年5月)/『マーケティングリサーチ入門』(高田博和 他著、PHP研究所、2008年12月)









