
Excelでできる!アンケート集計・分析の基本と実践テクニック
>>📥無料ダウンロード【お役立ち資料】エクセルでできるアンケートの集計と分析のやり方
目次[非表示]
はじめに
マーケティングにおいて、アンケート実施後の集計・分析作業は非常に重要です。できるだけ時間をかけず、コストもおさえて実施したい場合のおすすめの方法は、エクセル(Excel)を利用した集計・分析です。
この記事では、集計の基本となる、単純集計表、クロス集計表の作成方法から、グラフ化、分析ツールの使い方、さらに相関分析・回帰分析について、分かりやすく解説していきます。
この記事を読んで得られること
- Excelを使った単純集計、クロス集計、グラフ作成方法が分かる
- 基本統計量、相関・回帰分析について、Excelを使ったやり方が分かる
- 記事をまとめた資料がダウンロードできる(無料)
この記事をおすすめしたい方
- はじめてアンケート調査やネットリサーチを実施する方
- Excelを使ってアンケートの集計と分析を行いたい方
- アンケート結果をうまく活用したいと思っている方
※関連記事:🔗アンケートの作成方法を詳しく知る『アンケートの作り方|4つのコツと質問例(テンプレート)を大公開』
Excelで集計をする
アンケート実施後、その結果を活用できる形にするため、「単純集計」や「クロス集計」といった集計方法でデータを処理していきます。
以下の調査票(設問は2問)の場合を例として、詳しく解説していきます。
【Q1】あなたが最も好きなエナジードリンクを以下のうちからお選びください。(ひとつだけ) 1.商品A/2.商品B/3.その他/4.あてはまるものはない 【Q2】あなたがQ1で選んだエナジードリンク剤を購入するのは、どのオンラインショップですか?以下のオンラインショップのうちあてはまるものをすべてお選びください。(いくつでも) 1.ショップA/2.ショップB/3.ショップC/4.その他 /5.あてはまるものはない |
※集計方法のみ解説するため、選択肢数は絞り込み&「その他」の自由回答などは省略。
※全回答者数400人。
単純集計表の作成方法
まず初めに、単純集計表の作成方法について説明していきます。
単純集計(GT)とは、各設問の選択肢の数と割合(%)をそのまま集計した結果です。アウトプットは以下の通りになります。
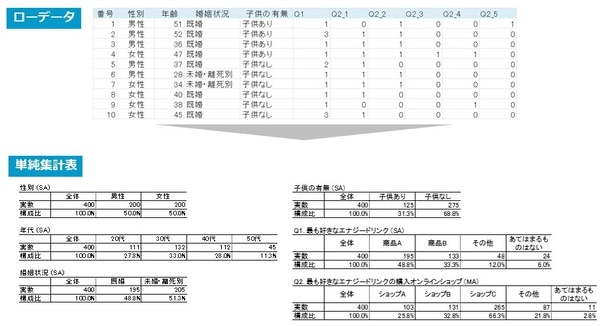
上記調査結果のローデータから、単純集計表を作ってみましょう。
手順1.ローデータの準備(項目とデータ形式)
まず、アンケート調査のローデータを用意します。
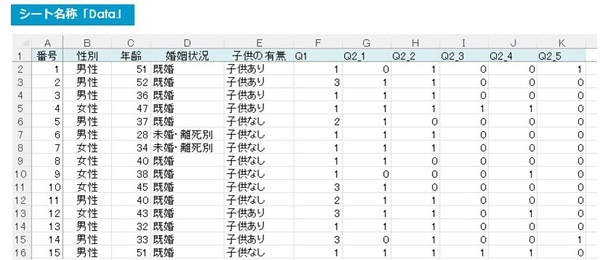
●表頭は「番号」「性別」「年齢」「婚姻状況」「子供の有無」で、これらA列~E列が回答者の属性です。
●F列:Q1の「最も好きなエナジードリンク」は、シングルアンサー(SA/単一回答)です(選択肢は1~4まで)。
●G列:Q2_1からQ2_5の「~どのオンラインショップですか?~」はマルチプルアンサー(MA/複数回答)のため、例えばQ2_1が選ばれた場合はG列に“1”、選ばれなかった場合はG列に“0”が入っています(ダミーデータとも呼ばれています)。
●全回答者数は400人ですので、A列「番号」は400まで続いています。
手順2.別シートに「単純集計表」のシートを作る
次に、ローデータのシート「Data」とは別シートに「単純集計」というシートを用意します。
単純集計表に必要な項目をリストアップし、各々、表のフォームを作成します。回答者数は400人ですので、実数の「全体」欄には「400」を入力しておきます。

手順3.“COUNTIF関数”で算出する
項目ごとに算出していきます。まず初めに「性別」の単純集計を算出してみましょう。
使用するのは「COUNTIF」関数です。
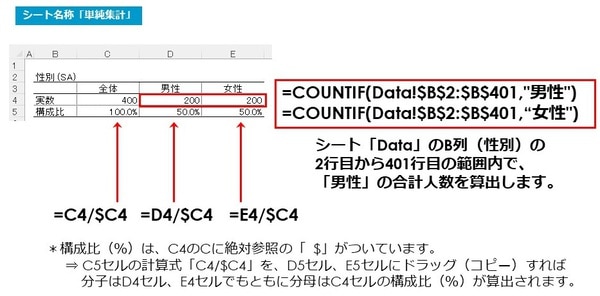
シート「Data」のB列(性別)の2行目から401行目の範囲内で、「男性」の合計人数を算出します。
シート「単純集計」の該当箇所(下の画像参照)に、
=COUNTIF(Data!$B$2:$B$401,“男性”)
を入力します。

男性と同様、シート「単純集計」の女性のセルにも、COUNTIF関数の、
=COUNTIF(Data!$B$2:$B$401,“女性”)
を入力します。
さらに構成比を算出するために該当箇所それぞれ(下の画像参照)に、計算式の、
=C4/$C4 =D4/$C4 =E4/$C4
を入力します。
手順4.“COUNTIF関数”で、他属性も算出する
「性別」に続き「婚姻状況」と「子供の有無」も、同様にCOUNTIF関数による単純算出が可能です。
シート「単純集計」の該当箇所に、COUNTIF関数の、
=COUNTIF(Data!$D$2:$D$401,“既婚”)
=COUNTIF(Data!$D$2:$D$401,“未婚・離死別”)
=COUNTIF(Data!$E$2:$E$401,“子供あり”)
=COUNTIF(Data!$E$2:$E$401,“子供なし”)
を入力します。

手順5.シングルアンサー(SA/単一回答)の単純集計をする(Q1)
次に、シングルアンサー(SA/単一回答)の単純集計のやり方です。
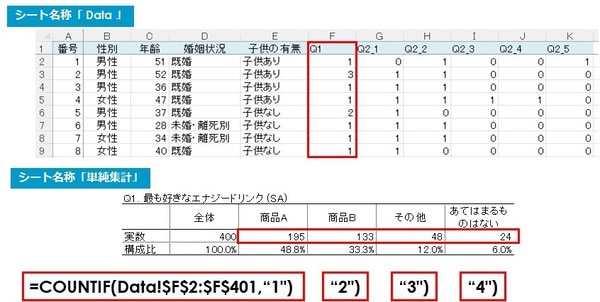
『【Q1】 好きなエナジードリンクの銘柄』の選択肢は、「1.商品A」から「4.あてはまるものはない」までの4段階でした。
シート「Data」のF列2行目から401行目までの範囲で、それぞれ1から4までの数値をカウントすれば、単純集計が完成します。
=COUNTIF(Data!$F$2:$F$401,“1”)
=COUNTIF(Data!$F$2:$F$401,“2”)
=COUNTIF(Data!$F$2:$F$401,“3”)
=COUNTIF(Data!$F$2:$F$401,“4”)
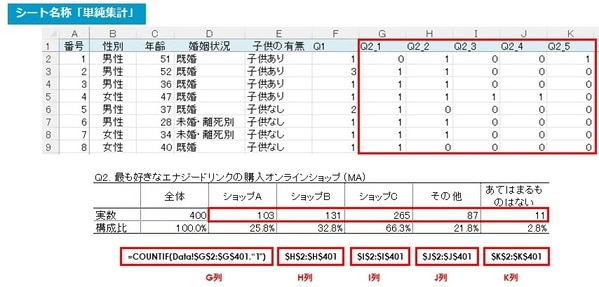
手順6.マルチプルアンサー(MA/複数回答)の単純集計をする(Q2)
マルチプルアンサー(MA/複数回答)の単純集計も、同じく「COUNTIF」関数を使います。
『【Q2】好きなエナジードリンクの購入オンラインショップ』では、5つの選択肢「Q2_1」から「Q2_5」まであり、各々1列ずつ、“0”、“1”、のダミーデータ形式になっています。
よって、“1”のデータの個数を加算すれば実数が算出されます。
G列 =COUNTIF(Data!$G$2:$G$401,“1”)
H列 =COUNTIF(Data!$H$2:$H$401,“1”)
I列 =COUNTIF(Data!$I$2:$I$401,“1”)
J列 =COUNTIF(Data!$J$2:$J$401,“1”)
K列 =COUNTIF(Data!$K$2:$K$401,“1”)
【Point!】年齢を年代にグループ化(COUNTIFS関数)
1歳毎の年齢を「20代」などの年代にまとめて単純集計表を作る方法も知っておきましょう。使う関数は「COUNTIF」の末尾に「S」がついた「COUNTIFS」関数です。
20代を集計する場合、シート「Data」のC列(年齢)の2行目から401行目の範囲内で、「20以上30未満」の人数を算出します。
シート「単純集計」の該当箇所(下の画像参照)に、
=COUNTIFS(Data!$C$2:$C$401,“>=20”,Data!$C$2:$C$401,“<30”)
を入力します。
この関数を30代、40代、50代のセルにドラッグしてコピー&ペーストします。
「30代」は「>=30」「<40」、「40代」は「>=40」「<50」、「50代」は「>=50」「<60」と年齢の数字を書き換えます。

【Point!】ピボットテーブルによる集計のやり方
COUNTIF関数と合わせて、ピボットテーブルによる集計のやり方も知っておくと、非常に重宝します。あらかじめフォームを作って関数で算出したほうが便利ではありますが、関数で算出したデータの検証のためにピボットテーブルを使うケースもあるからです。
ピボットテーブルの使い方は、お役立ち資料(無料・画像付き)で詳しく解説していますので、是非参考にしてください。
>>📥『ピボットテーブルによる単純集計のやり方』を知る【資料を無料ダウンロード】
クロス集計表の作成方法
単純集計表に続き、次はクロス集計表の作成方法について解説していきます。
>>🔗クロス集計について詳しく知る【クロス集計とは│エクセルのクロス集計表作成と分析のやり方】
先述の「単純集計表の作成」と重複しますが、調査票例を再掲載いたします。
【Q1】あなたが最も好きなエナジードリンクを以下のうちからお選びください。(ひとつだけ) 1.商品A/2.商品B/3.その他/4.あてはまるものはない 【Q2】あなたがQ1で選んだエナジードリンク剤を購入するのは、どのオンラインショップですか?以下のオンラインショップのうちあてはまるものをすべてお選びください。(いくつでも) 1.ショップA/2.ショップB/3.ショップC/4.その他 /5.あてはまるものはない |
※集計方法のみ解説するため、選択肢数は絞り込み&「その他」の自由回答などは省略。
※全回答者数400人。
クロス集計表のアウトプットは以下のようになります。
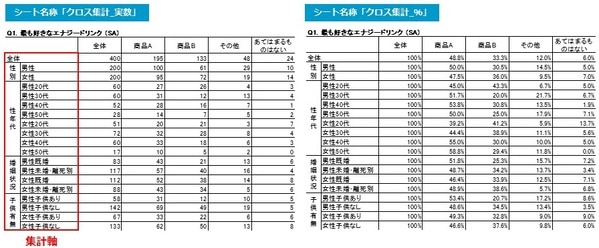
こちらの例では「実数」と「構成比(%)」を別表(別シート)にしていますが、一つの表の上部に「実数」・下部に「構成比(%)」を配置するケースもあります。
●表側は「全体」の他、「性別」「性年代」「婚姻状況」「子供有無」の4項目を「クロス集計軸」としました。
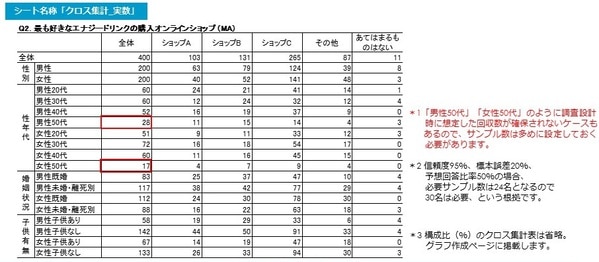
●クロス集計軸は、通常「集計軸」と呼ばれ、“調査目的を達成するために、どのような属性の人々のデータが必要か”という重要な項目のことで、アンケートの配信前の調査設計時に決めておくことが理想的です。調査目的達成のため、必要な属性の人たちのデータを、どの程度回収できるか把握しておく必要があるからです。
この例の集計軸の場合、性年代で男女ともに「50代」の回答者数が「28名、17名」と、一般的に集計に必要とされる最低限の30名を下回っており(*2)、「男性50代」と「女性50代」は、レポート(報告書)では「参考値」としなければなりません。
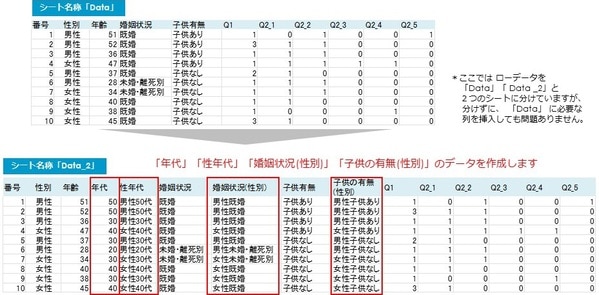
手順1.ローデータを加工する
単純集計と同様に、アンケート調査のローデータを用意し、集計軸となる項目の列を加えます。クロス集計ではローデータの加工が必要となります。
単純集計表の年代では関数を使って年齢から算出しましたが、クロス集計では表側の集計軸を使用するため、あらかじめデータを作成する必要があります。
※ここではローデータをシート「Data」「Data_2」と2つのシートに分けていますが、分けずに「Data」に必要な列を挿入しても問題ありません。
手順2.シングルアンサー(SA/単一回答)のクロス集計をする(Q1)
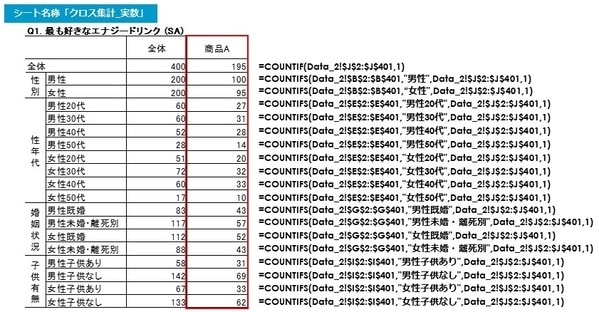
以下は「商品A」の各セルに入る関数です。「全体」のみ「COUNTIF」関数、他の集計軸は全て「COUNTIFS」関数となります。
「商品B」「その他」「あてはまるものはない」については、この「商品A」の関数をドラッグして貼り付け、最後の数字をそれぞれ「,2)」「,3)」「,4)」と手入力で上書きします。
手順3.マルチプルアンサー(MA/複数回答)のクロス集計をする(Q2)
以下は「ショップA」の各セルに入る関数です。「全体」のみ「COUNTIF」関数、他の集計軸は全て「COUNTIFS」関数となる点は、前述の単数回答と同様ですが、複数回答は“0”、“1”、のダミー変数なので、“1”の個数をカウントします。
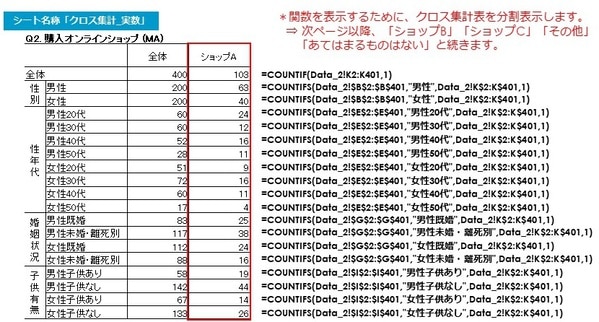
以下は「ショップB」の各セルに入る関数です。
前述の「ショップA」と同様ですが、「ショップB」は「L列」なので「1」の合計がカウントされるのは「L列」です。
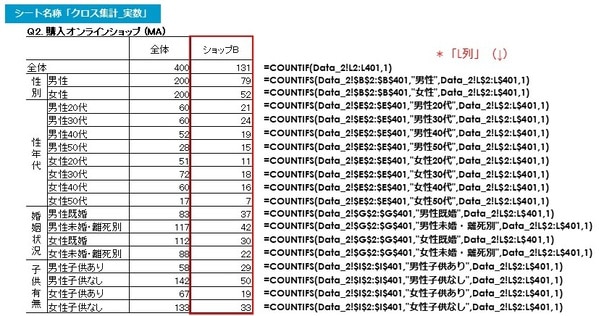
以下は「ショップC」の各セルに入る関数です。
前述の「ショップA」と同様ですが、「ショップC」は「M列」なので「1」の合計がカウントされるのは「M列」です。
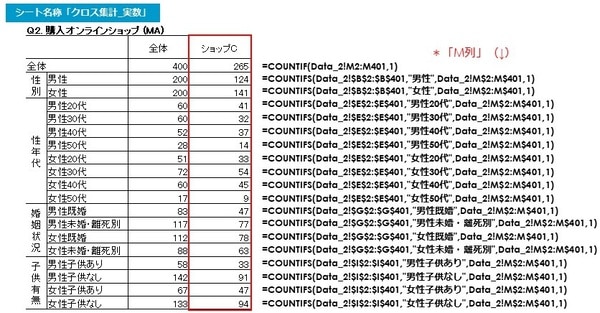
以下は「その他」の各セルに入る関数です。
前述の「ショップA」と同様ですが、「その他」は「N列」なので「1」の合計がカウントされるのは「N列」です。
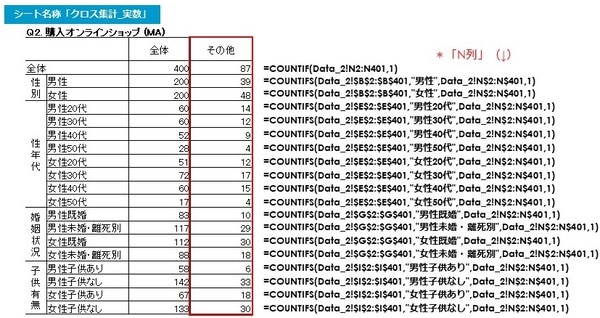
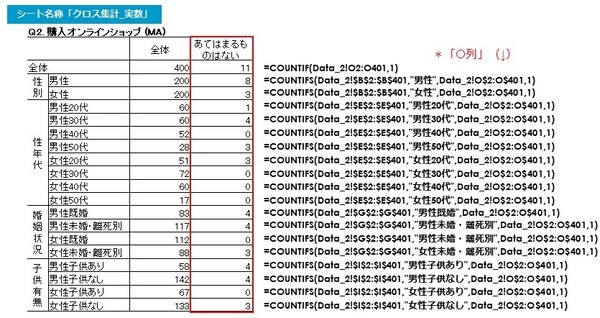
以下は「あてはまるものはない」の各セルに入る関数です。
前述の「ショップA」と同様ですが、「あてはまるものはない」の合計がカウントされるのは「O列」です。
手順4.シングルアンサーのクロス集計表をグラフ化する(Q1)
続いて、Q1の「シングルアンサー(SA/単一回答)」のクロス集計表をデータを可視化するためにグラフ化します。ここでは、「性年代別」のグラフを作成します。
①グラフ作成用の表を作成~デフォルトの帯グラフの完成
まず、グラフ作成用の表を作成し、クロス集計表のシート「クロス集計_%」の“構成比(%)”を『参照』させます(「値貼り付け」でもかまいません)。
※クロス集計表のシート「クロス集計_%」の“構成比(%)”をそのままグラフの参照元とするのではありません。
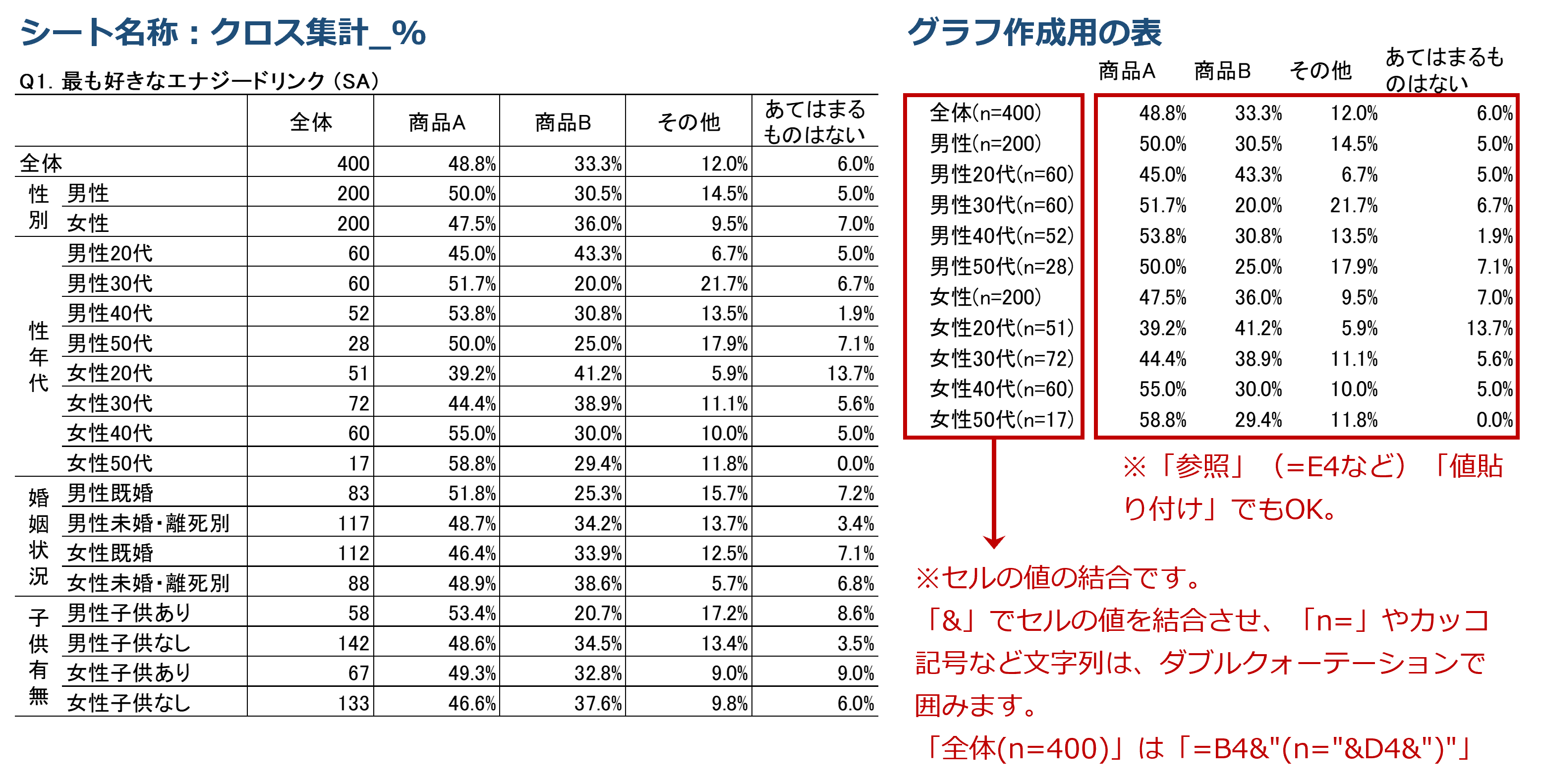 こちらを元にして、合計が100%になるデータの比較になるため、帯グラフを作ります。
こちらを元にして、合計が100%になるデータの比較になるため、帯グラフを作ります。
《1》「挿入」画面で、グラフ作成用の表を「範囲指定」
《2》「グラフ」の右下をクリック
《3》「すべてのグラフ」から「横棒」→「100% 積み上げ横棒」をクリック
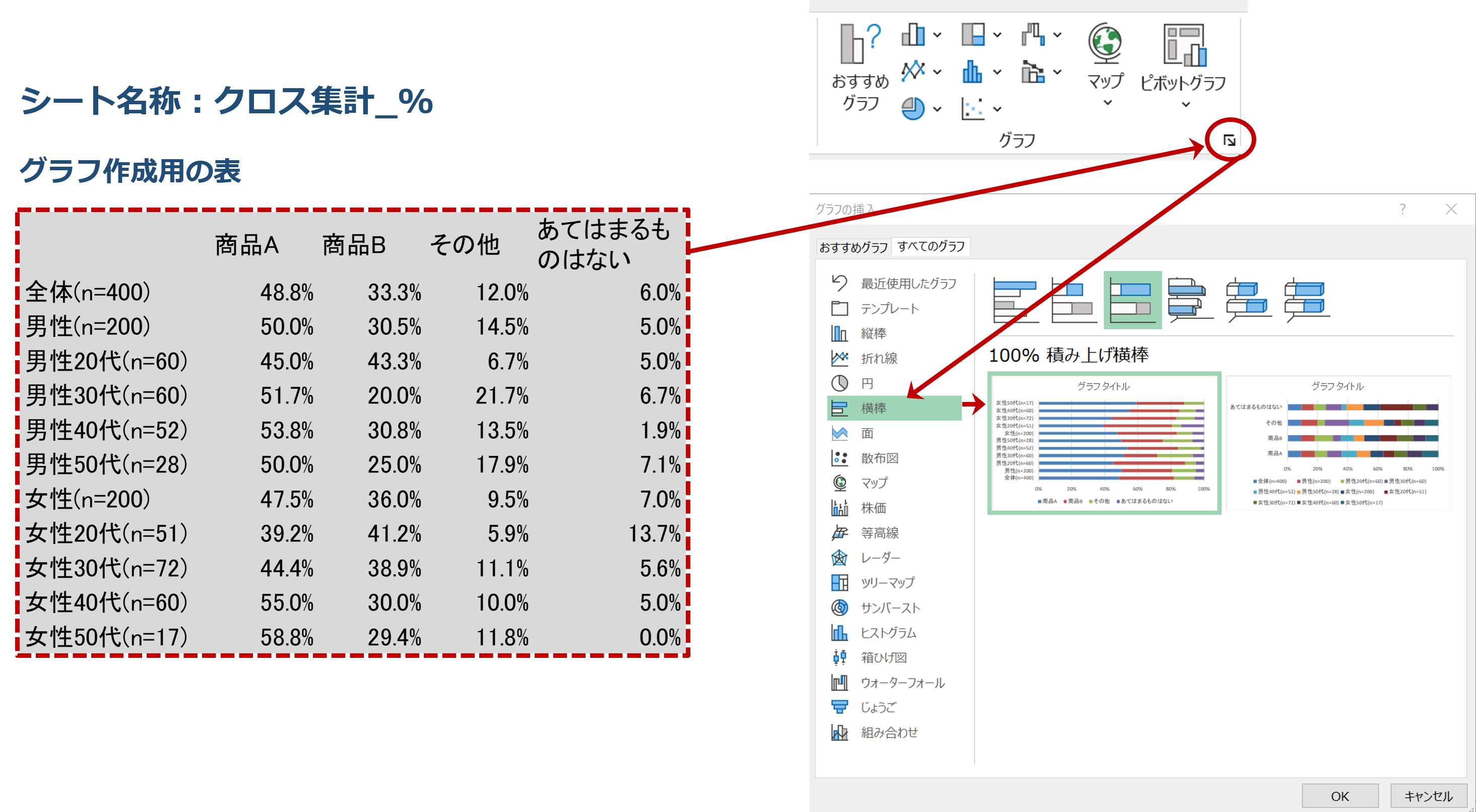
ここまでの処理が終わると、デフォルトで帯グラフが作成されます。下図右側が完成した帯グラフです。
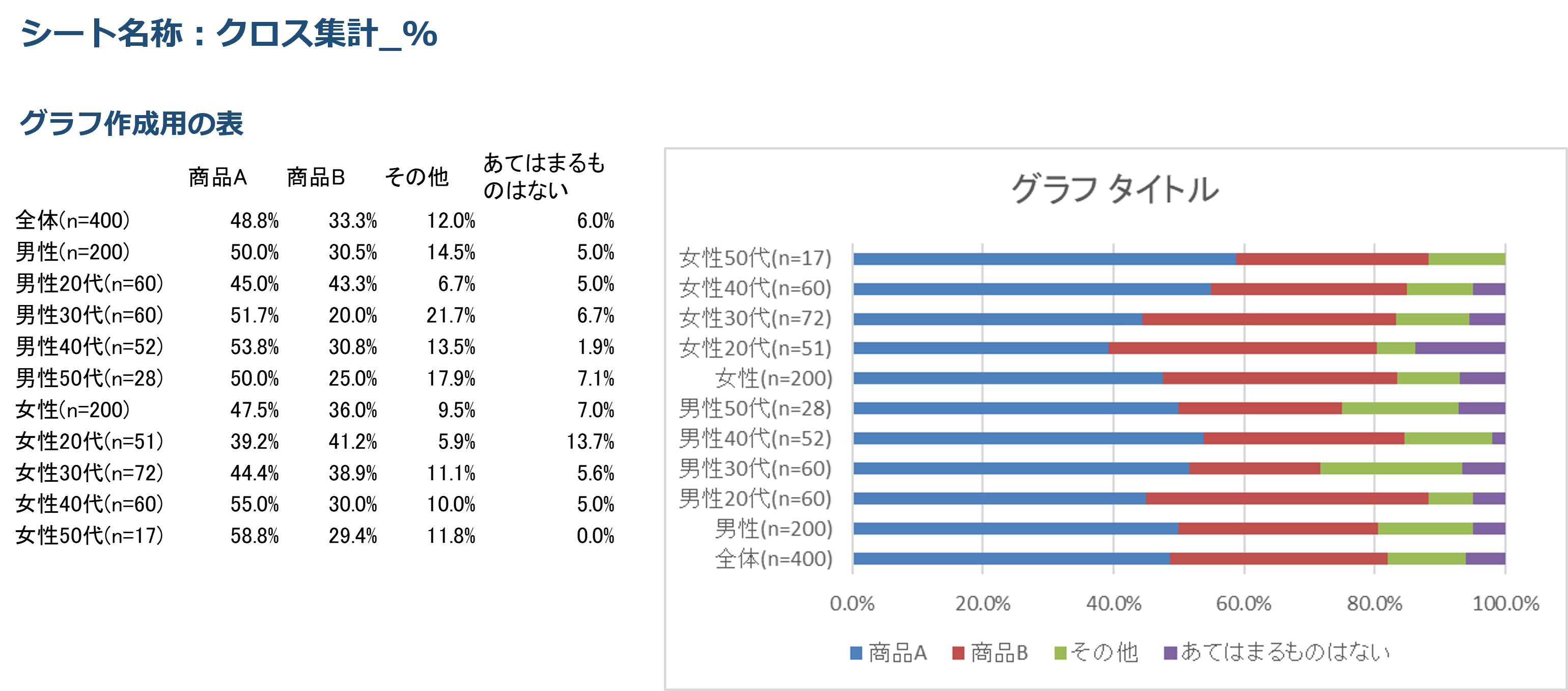
②デフォルトの帯グラフを整形する
次に、デフォルトで作成された帯グラフを整形します。
グラフの整形は、グラフエリアの中の該当する箇所をクリックしてアクティブ化し、右クリックで「書式設定」のボックスが画面右側に表示されることで、操作することができます。
《1》グラフエリアの塗りつぶしと枠線を消します。
《2》タイトルを手入力します(「グラフ タイトル」にそのまま上書きします)。
《3》クロス表と同じように「全体」が最上部、「女性50代」が最下部になるよう、「軸の書式設定」で「軸を反転」させます。
《4》凡例の表示位置を最下部から最上部にします。
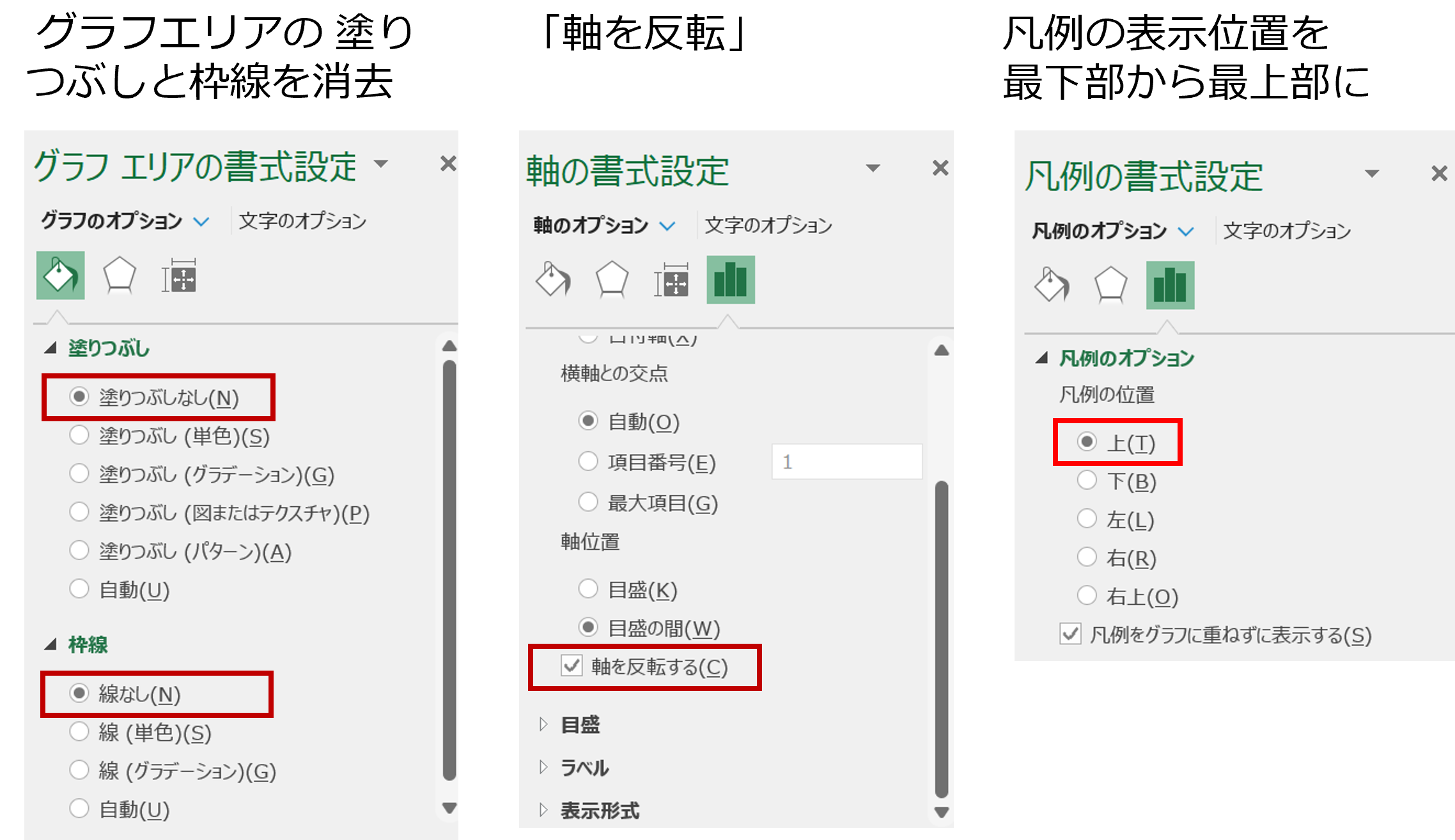
《5》グラフの色(トンマナ)がうるさいので、寒色系に変えます。
《6》データラベル(%の数字)を入れるため、グラフの帯の幅を広げます。
《7》データラベル(%の数字)を入れます。
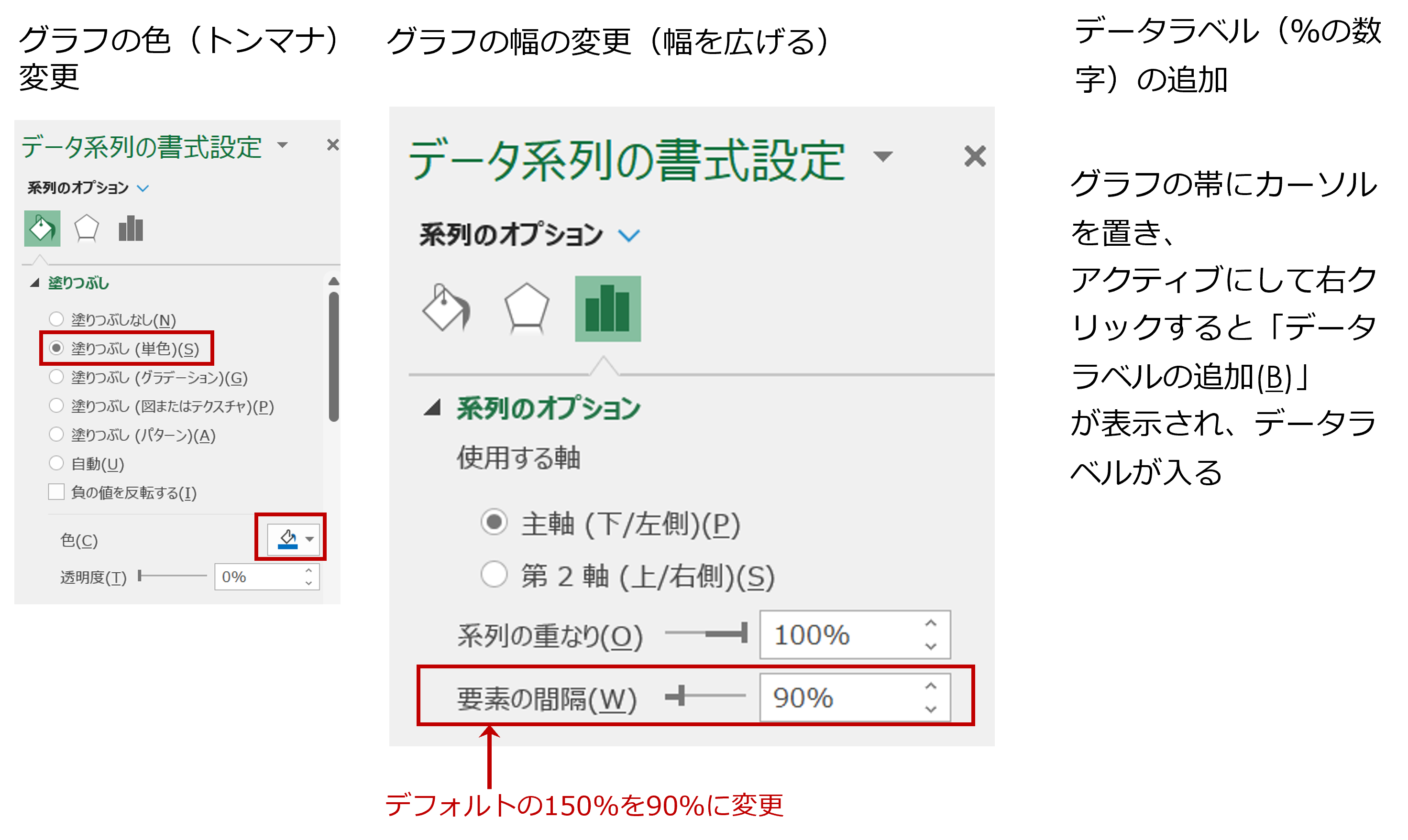 ここまでの手順で完成したシングルアンサー(SA/単一回答)のクロス集計表のグラフがこちらです。
ここまでの手順で完成したシングルアンサー(SA/単一回答)のクロス集計表のグラフがこちらです。
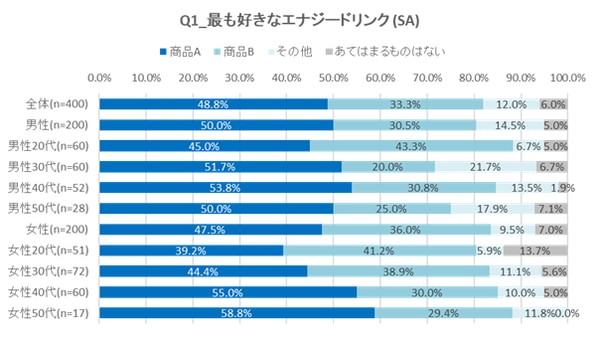
手順5.マルチアンサーのクロス集計表をグラフ化する(Q2)
続いて、Q2の「マルチアンサー(MA/複数回答)」のクロス集計表をグラフ化していきましょう。ここでも「性年代別」のグラフを作成します。
①グラフ作成用の表を作成~デフォルトの折れ線グラフの完成
シングルアンサーと同様に、構成比(%)のクロス集計表のデータをそのままグラフの参照元とするのではなく、グラフ作成用の表を作成し、クロス集計表のシート「クロス集計_%」の“構成比(%)”を『参照』させます(「値貼り付け」でもかまいません)。
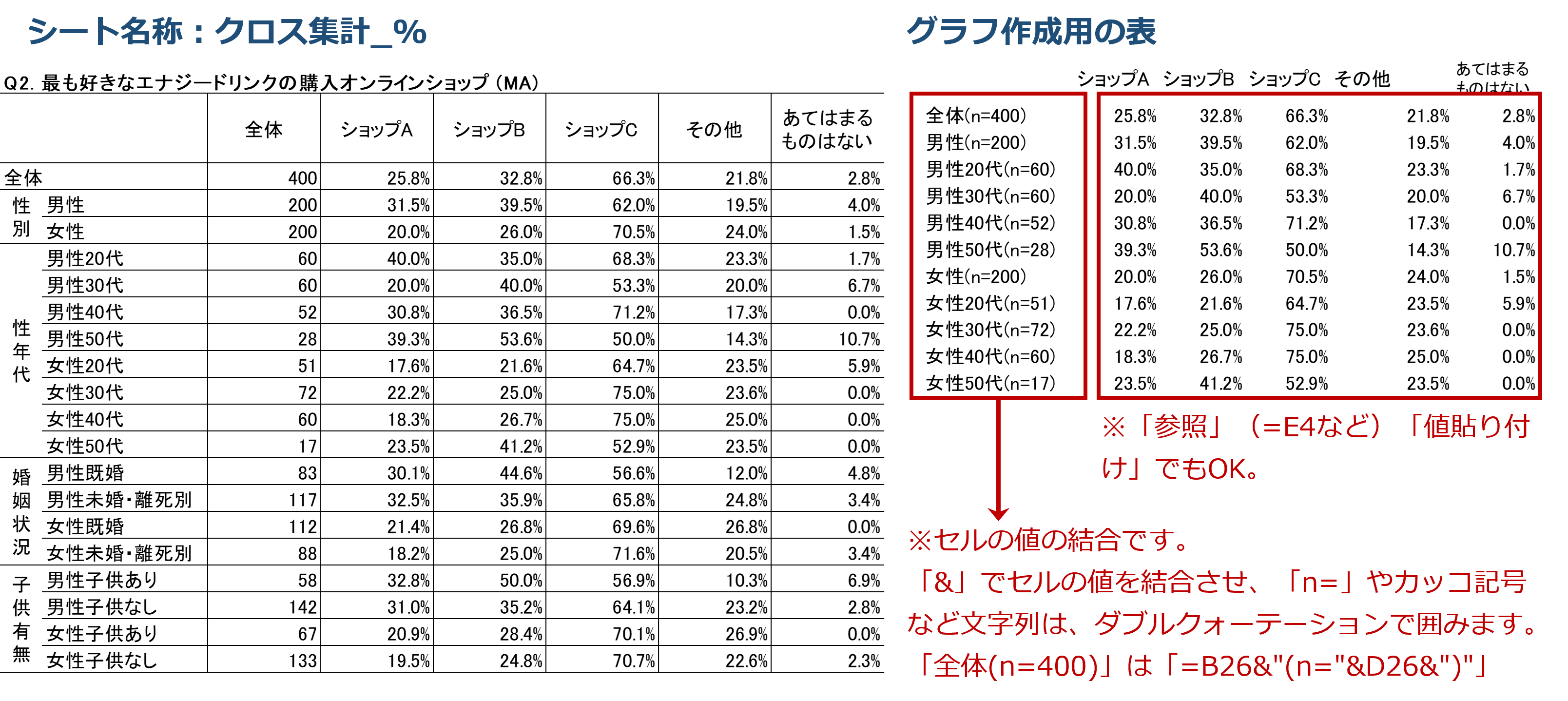
合計が100%にはならないデータの比較になるため、折れ線グラフにします。
属性の中の比較、例えば男性の中でどのオンラインショップでの購入が多いのか?を比較するのには棒グラフが適していますが、ここでは属性の間の比較、例えば「男性20代と30代の間でのショップ購入の違い」にフォーカスを当てるため、折れ線グラフの方が適しています。
《1》「挿入」画面で、グラフ作成用の表を「範囲指定」
《2》「グラフ」の右下をクリック
《3》「すべてのグラフ」から「折れ線」→「100% 積み上げ横棒」をクリック
ここまでの処理が終わると、デフォルトで折れ線グラフが作成されます。下図右側が完成した帯グラフです。
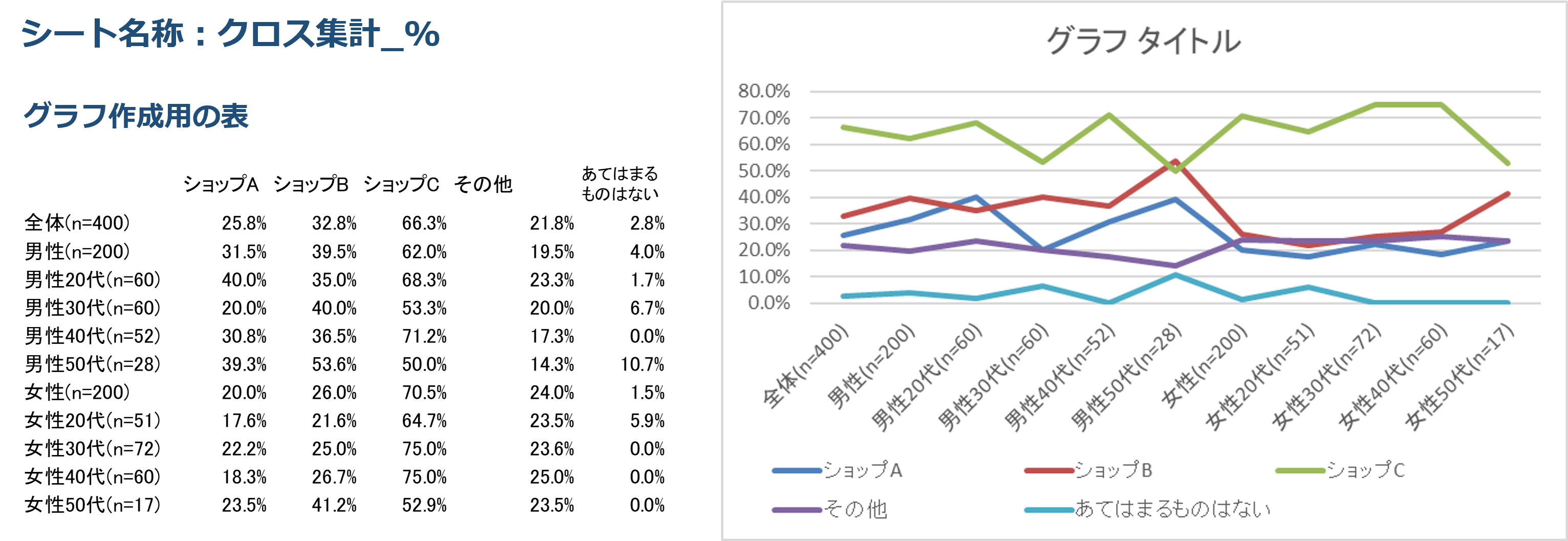
②デフォルトの折れ線グラフを整形する
次に、デフォルトで作成された折れ線グラフを整形します。
《1》グラフエリアの塗りつぶしと枠線を消します。
《2》タイトルを手入力します(「グラフ タイトル」にそのまま上書きします)。
《3》凡例の表示位置を最下部から最上部にします。
《4》折れ線の色(トンマナ)を変えます。
《5》データラベル(%の数字)を入れます。
《6》その他、軸の項目名や目盛りラベルの文字の大きさを微調整します。
※書式設定は、シングルアンサーの帯グラフの整形の場合と基本的に変わりません。グラフの軸や折れ線などをクリックし、アクティブにしながら、「書式設定」のボックスの項目を調整してみてください。
ここまでの手順で完成したマルチアンサーのクロス集計表のグラフがこちらです。
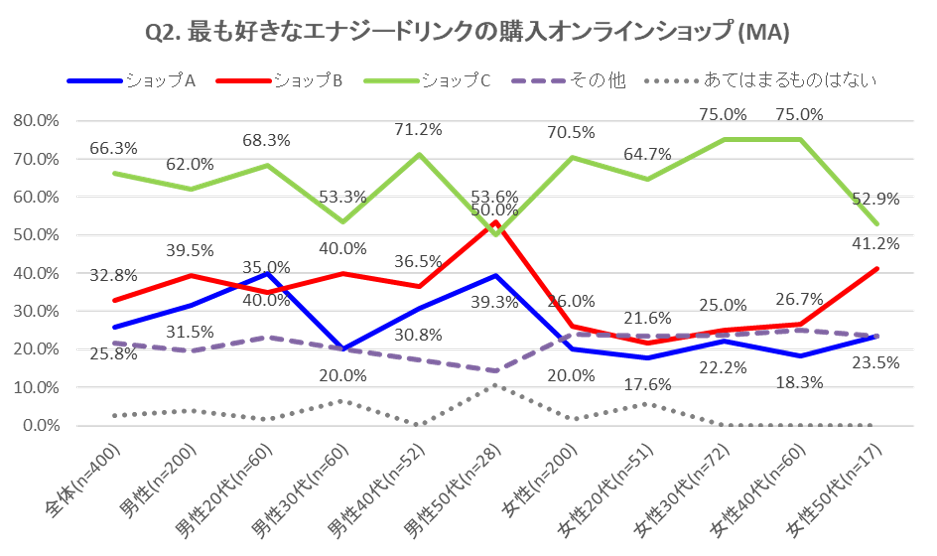
【Point!】クロス集計もピボットテーブルで集計できる
単純集計と同様、クロス集計もピポットテーブルで集計することができます。
クロス集計におけるピボットテーブルの使い方も、お役立ち資料(無料・画像付き)で詳しく解説していますので、是非参考にしてください。
>>📥『ピボットテーブルによるクロス集計のやり方』を知る【資料を無料ダウンロード】
集計作業を補助する機能の一例
アンケート結果をExcelで分析する前に、集計内容を事前に確認できると安心です。
セルフ型アンケートツール「Freeasy」では、CSV形式での出力に加えて、Web上で集計や加工ができる「&cross(アンドクロス)」という機能が提供されています。
単純集計やクロス集計、テキスト回答の整理などが可能で、Excelでの分析に入る前の確認や補助的な集計手段としても活用できます。
詳細な分析はExcelで行う前提でも、こうした機能を知っておくことで、作業の精度や効率が高まる場面もあるかもしれません。
>>🔗機能の概要はこちら →「Freeasy &crossの詳細を見る」
Excelで分析をする
集計が完了したら、次に分析をおこないます。「分析」と聞くと統計学など難しい内容を思い浮かべるかもしれませんが、実際には難しく考える必要はありません。
特に、エクセルに備わっている「分析ツール」を活用すれば、誰もが手軽に相関分析や回帰分析をおこなうことが可能です。
はじめに│Excelの「分析ツール」を表示する方法
《1》ファイルメニューをクリック
《2》ファイルメニューで「その他」 「オプション」をクリック
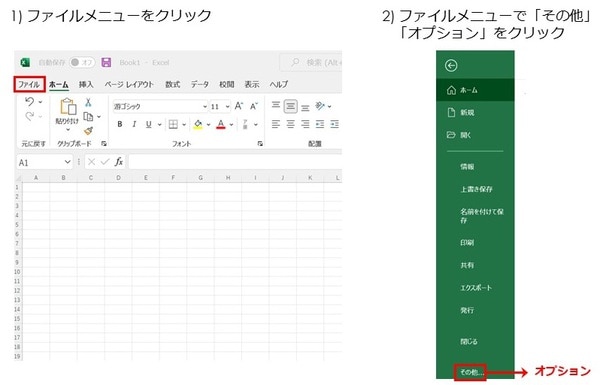
《3》「エクセルのオプション」画面の「アドイン」をクリック
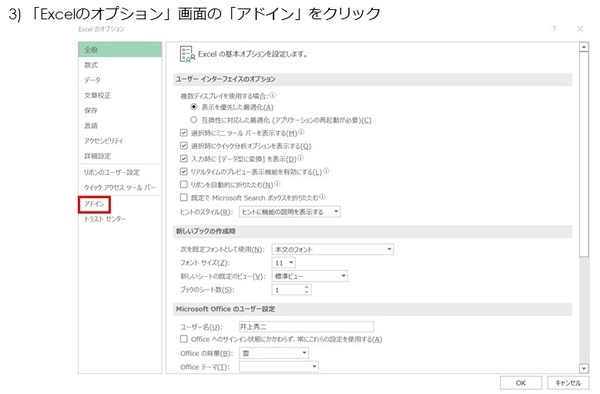
《4》「アドイン」画面で「分析ツール」をクリックした後、「設定」をクリック
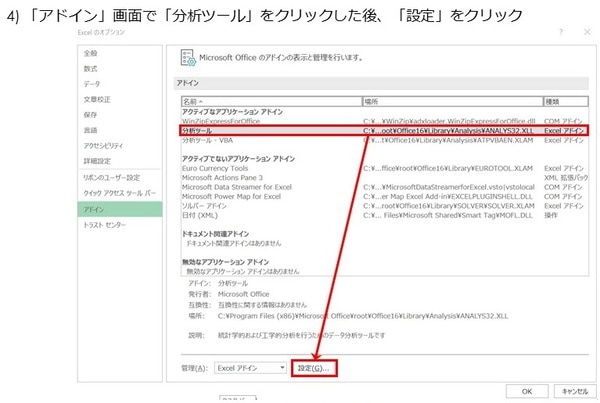
《5》この画面で「分析ツール」にチェックを入れる(完了)
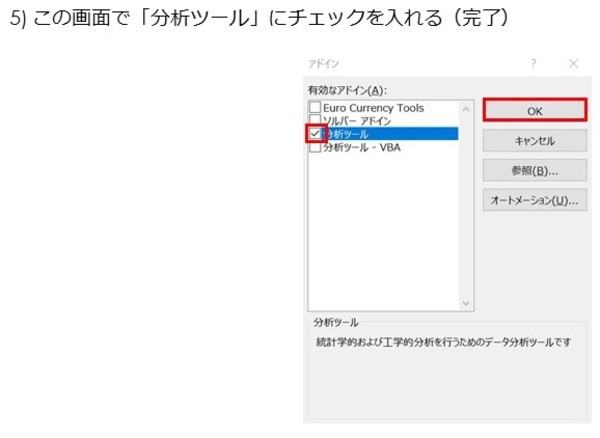
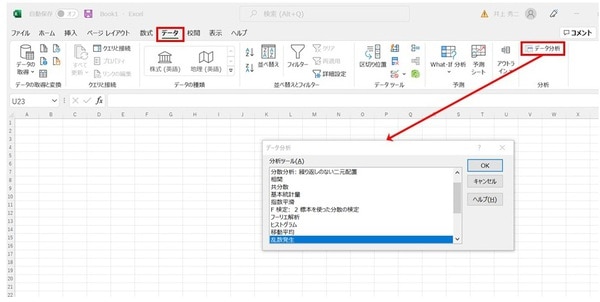
ここまでの手順で、Excelの「データ」画面で、「データ分析」ツールが使えるようになりました。
画面右側の「データ分析」をクリックすると、「データ分析」のボックスが表示されます。
基本統計量の算出方法
「基本統計量」とは、そのデータの基本的な特徴(特性)を表す数値のことです。
そのデータが全体的にどのような特徴があるのかを把握することができるため、この基本統計量をもとに、データを分析をしていくことが可能となります。
ここでは例として、アンケート調査結果の統計情報を確認し、相関分析と回帰分析を試みます。
設問は、以下の2問です。
【Q1】あなたはこの飲料○○○○をどの程度好きですか。(ひとつだけ) <好意度> 1.非常に好き/2.好き/3.やや好き/4.どちらともいえない/5.やや嫌い/6.嫌い/7.非常に嫌い 【Q2】あなたが感じる飲料○○○○の印象を教えてください。(いくつでも) <香味特性> 香り/苦み/甘み/酸味/味の濃さ/飲みごたえ/後味/口当たり/まろやかさ/すっきり/軽さ/クセ <選択肢> 1.とてもそう感じる/2.そう感じる/3.ややそう感じる/4.どちらともいえない/5.あまりそう感じない/6.そう感じない/7.とてもそう感じない |
※集計方法のみ解説するため、選択肢数は絞り込み、「その他」の自由回答などは省略。
※全回答者数は400名
手順1.ローデータを加工する
全回答者数は400名なので、ローデータの行数は401行、A列の「番号」は400まで続きます。
C列の「好意度」、D列からO列の「香味特性」はともに、選択肢の値が小さいほど評価が高く、大きいほど低評価でした。
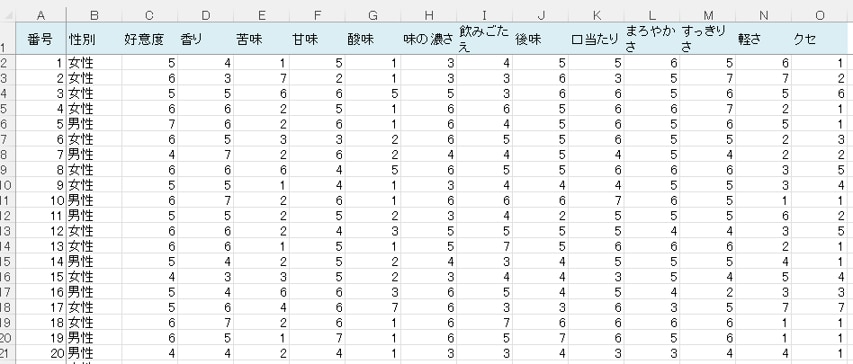
相関分析や回帰分析を行う際、値が大きいほど評価が高いほうが分かりやすいため、上のローデータでは、好意度・香味特性ともに「1」が最も低評価で「7」が最も高評価となるようにデータを変換しています。
※【Point】相関分析や回帰分析では、あらかじめ調査設計時に、好意度と香味特性の選択肢のスケール(7段階の選択肢など)を合わせておく必要があります。
手順2.基本統計量を算出する
データの全体像である「基本統計量」を算出しましょう。
まず、【Q1】の「好意度」の基本統計量を表示させます。
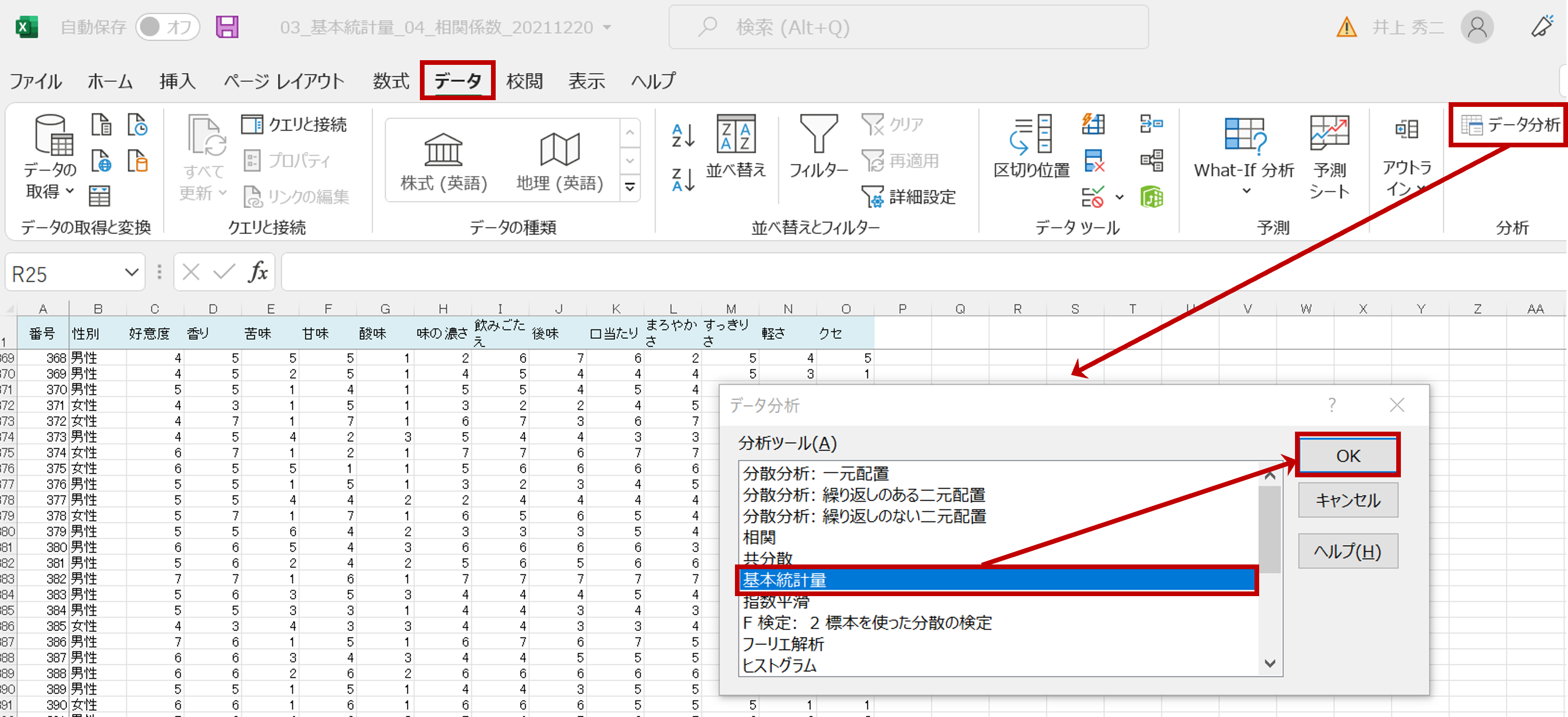
「データ」画面で「データ分析」をクリックすると、「データ分析」のボックスが表示されます。ここで「基本統計量」を選び「OK」をクリックします。
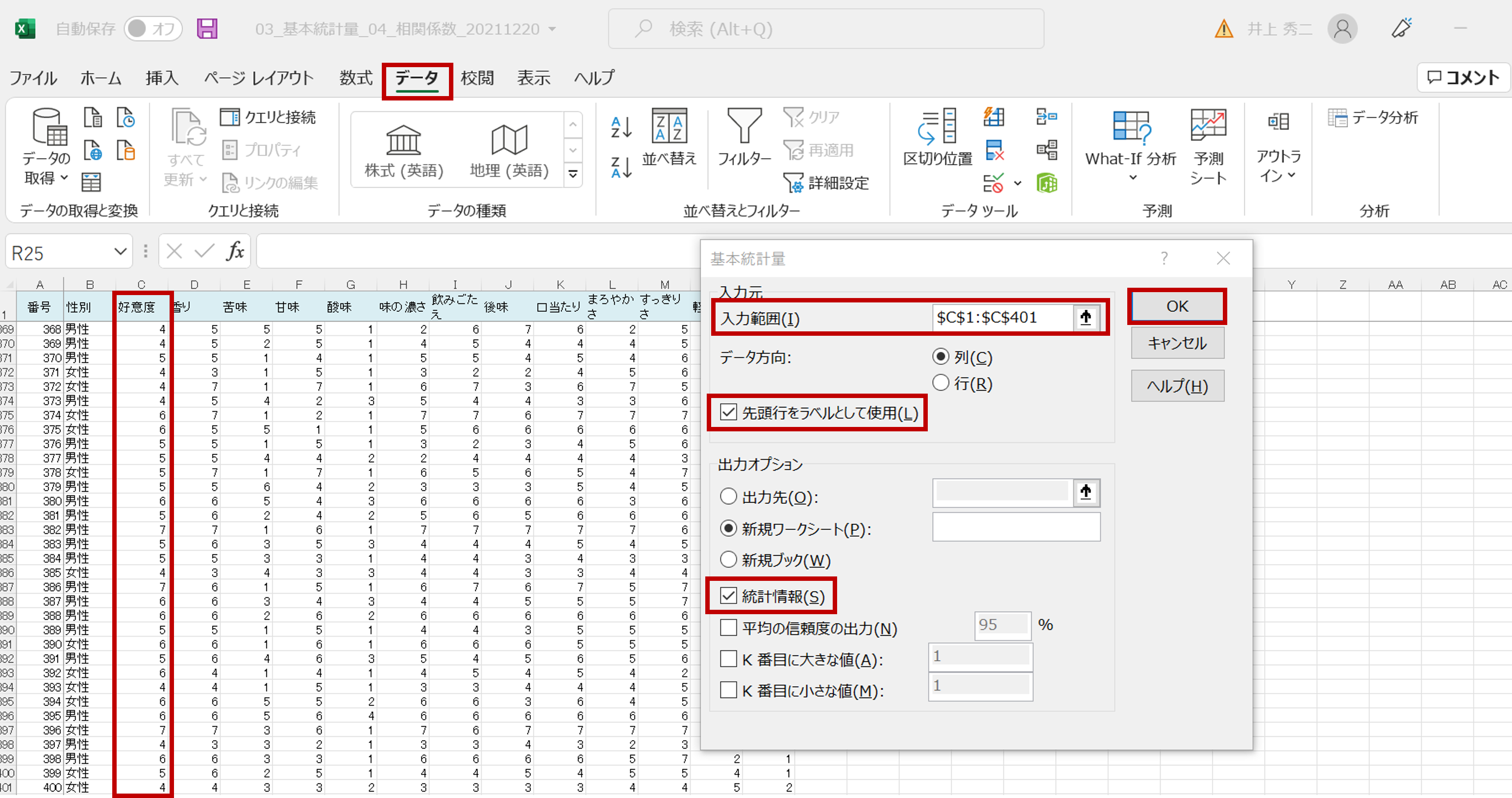
「基本統計量」のボックスにて、まず「入力範囲」を指定します。
※「好意度」はC列1行から401行までが範囲です(絶対参照の「$」は自動的に付きます)。
※「先頭をラベルとして使用(L)」「統計情報(S)」も、忘れずにチェックを入れます。
手順3.基本統計量の主要指標と見方を理解する
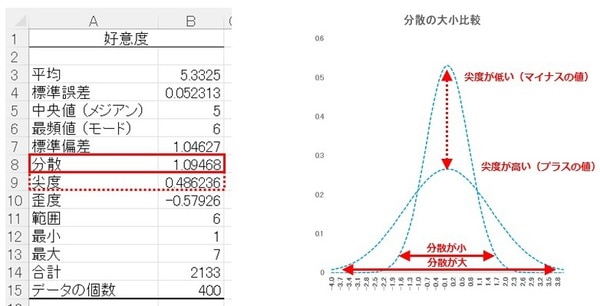
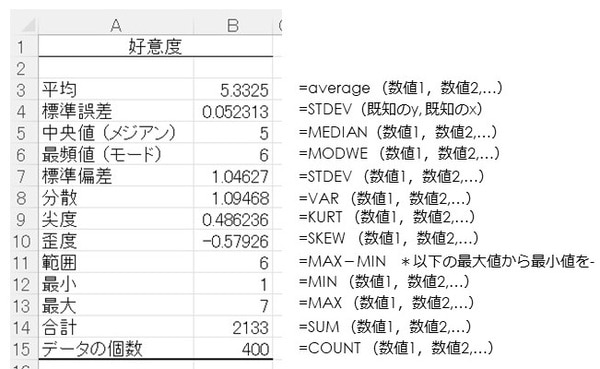
アウトプットは下記のとおりです。
基本統計量では、平均値をはじめとして「代表値」が表示されます。

各指標の意味
- 平均:データを全部足してデータ数で割った算術平均。
- 標準誤差:平均値の信頼性と確実性を表す指標。
- 中央値(メジアン):データを数値の大きい順に並べたときの中央の数値。
- 最頻値(モード):データの中で最も多い数値。
- 標準偏差:データのバラツキ具合のこと。分散(下記参照)の正の平方根(SD)。
- 分散:データのバラツキ具合のこと。平均からどの程度、離れているかを表す。
- 尖度:正規分布(尖度=0)に対し、正の場合はスソが広く、負の場合は尖る。
- 歪度:正規分布(歪度=0)の左右対称からのズレで、1.0を超えていたら要注意。
- 範囲:データの最小値と最大値のレンジ。
- 最小・最大:データの最小値と最大値(Q1.はカテゴリーデータであり、1~7まで)。
データ分析を行う場合、一般的には、真っ先に「平均値(算術平均)」を求めますが、もしこの「平均値」が、「中央値」や「最頻値」と大きく離れていたら要注意です。
分散と標準偏差
データがどの程度散らばっているのか、バラつき具合が分かる重要指標が「分散」です。
ただし「分散」は計算過程で数値を2乗しているため、単位を変えてよりわかりやすくし、他指標と比較しやすい単位に計算して重宝されている指標が「標準偏差」です。
「平均値から標準偏差±1個分の範囲内に7割のデータがある」といったように表現されることもあります。
分散と尖度
前述のとおり、データのバラつき具合を見る指標は「標準偏差」ですが、その素は「分散」です。
分散が大きいとデータはより広くバラつき、分散が小さいとバラつきは狭くなり、代わりに「尖度(せんど)」が低くなります。
「尖度」が低くなると、右下のグラフのように頂点が高く尖った形となり、平均値の周辺にデータが多く集まっている、つまり「分散」が小さい、ということになります。
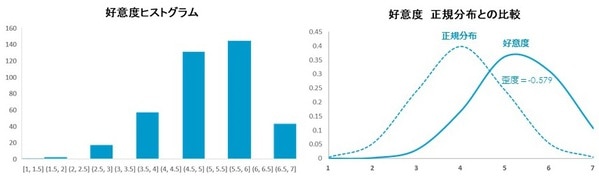
手順4.ヒストグラムによる正規分布との比較をする
【Q1】の好意度のデータをヒストグラムにすると下図のようになります(「挿入」画面の「グラフ」)。ひと目でデータが4.5から6までの高評価に偏っていることがわかります。
この【Q1】の好意度ヒストグラムを、散布図グラフにして正規分布グラフと比較したのが、右側の散布図です。歪度が-0.579とマイナスなので、正規分布より”右側に山ができ上っている形”となっています。
歪度の絶対数が「1」を超えると正規分布とのズレが問題となりますが、-0.579なので妥当なところでしょう。
【参考】関数による基本統計量の算出方法
基本統計指標のうちピンポイントで、例えば「中央値」だけを見ておきたいという場合は、ローデータの範囲(行・列)を指定し、関数で算出する方法がおすすめです。
Excelの「数式」画面で「関数ライブラリ」を参照すれば、各関数のデータ範囲や引数がボックス表示で入力できるようになっています。
※以下には詳細は記さず、関数の名称のみ記載いたします。
Excelの相関分析のやり方
はじめに│相関係数について理解する
相関分析では、0〜1の範囲で示される「相関係数(そうかんけいすう)」が指標となります。
相関係数とは、2種類のデータの直線的な関係の強さを表す指標のことです。1に近いほど強い相関があり、0に近いほど相関は弱くなります。
相関係数がプラスの場合は「正の相関」と呼ばれ、一方の値が高くなるともう一方も高くなる傾向があります。逆にマイナスの場合は「負の相関」となり、一方が高くなるともう一方は低くなる傾向を示します。
なお、データ同士に相関関係が見られても、それが必ずしも原因と結果を示す「因果関係」であるとは限らないため、注意が必要です。これは調査現場でもよく言われるポイントです。
とはいえ、相関のない因果関係はほとんど存在せず、データ同士の「関連性」を相関分析によって明らかにすることは、データ分析において非常に重要なステップです。
手順1.相関行列表を作る
ここでは、「【Q1】好意度」と「【Q2】香味特性」の、全データ間の相関係数を求めてみましょう。
「データ」画面で「データ分析」をクリックすると、「データ分析」のボックスが表示されます。ここで「相関」を選び「OK」をクリックします。
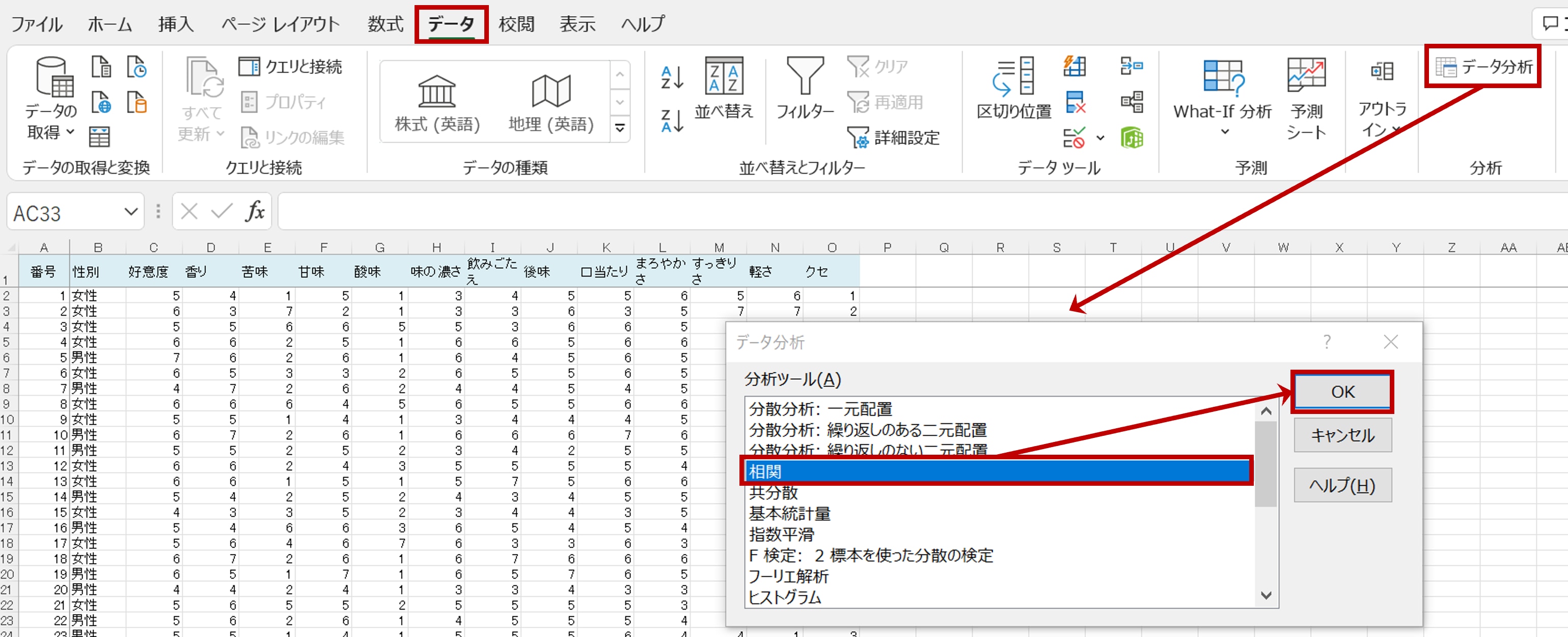
「相関」のボックスが表示されたら、最初に「入力範囲」を指定します。
「好意度」と「香味特性」全て、C1列からO列401までの範囲です(絶対参照の「$」は自動的に付きます)。
「先頭をラベルとして使用(L)」にチェックを入れたら、「OK」をクリックします。
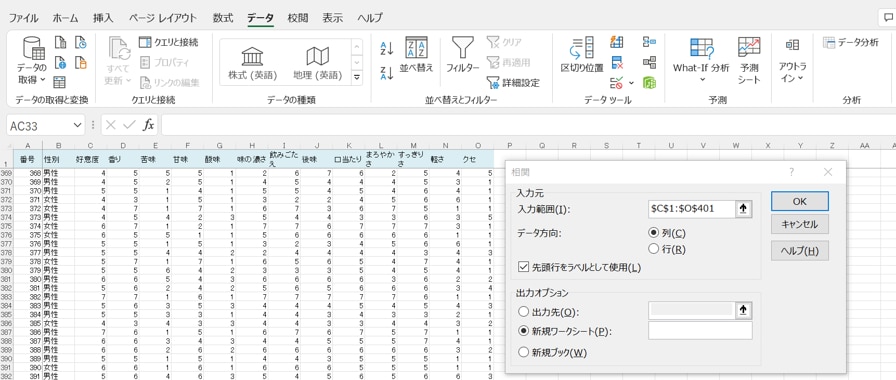
「出力オプション」でデフォルトの「新規ワークシート」のまま「OK」をクリックすると、別シートに「相関行列表」が作成されました。下記が「相関行列表」です。
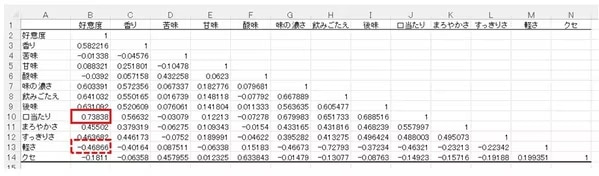
手順2.相関行列表から分析する
前述の通り、相関係数は、1に近いほど強い相関があり、0に近いほど相関は弱くなることから、こちらの「相関行列表」より、結果、好意度との正の相関が最も強い香味特性は「口当たり」、逆に負の相関が最も高いのは「軽さ」ということがわかりました。
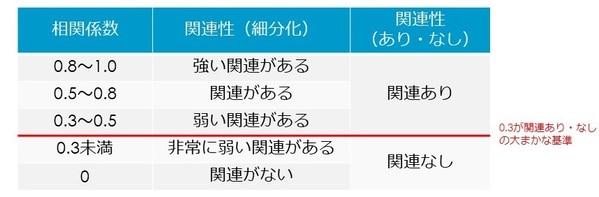
【参考】相関係数の基準について
相関関係の強弱には、統計的に明確な基準はあるわけではありません。対象となるカテゴリーによっても異なり、都度、分析者の判断が求められます。以下の目安はあくまでも参考として捉えるのが適切です。
Excelの回帰分析のやり方
はじめに│回帰分析について理解する
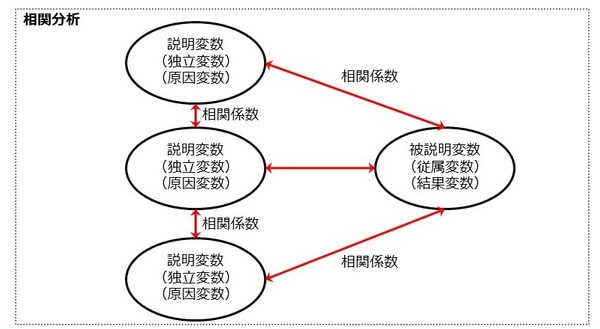
回帰分析は、原因となる「説明変数」から、結果となる「被説明変数」を導き出す計算式を算出する(モデル化)分析方法です。
多くの場合、回帰分析は予測モデルとして使われますが、アンケート調査結果などカテゴリーデータでもモデルを作ることはできます。
以下は、回帰分析のイメージです。1対1が「単回帰分析」、多対1が「重回帰分析」です。
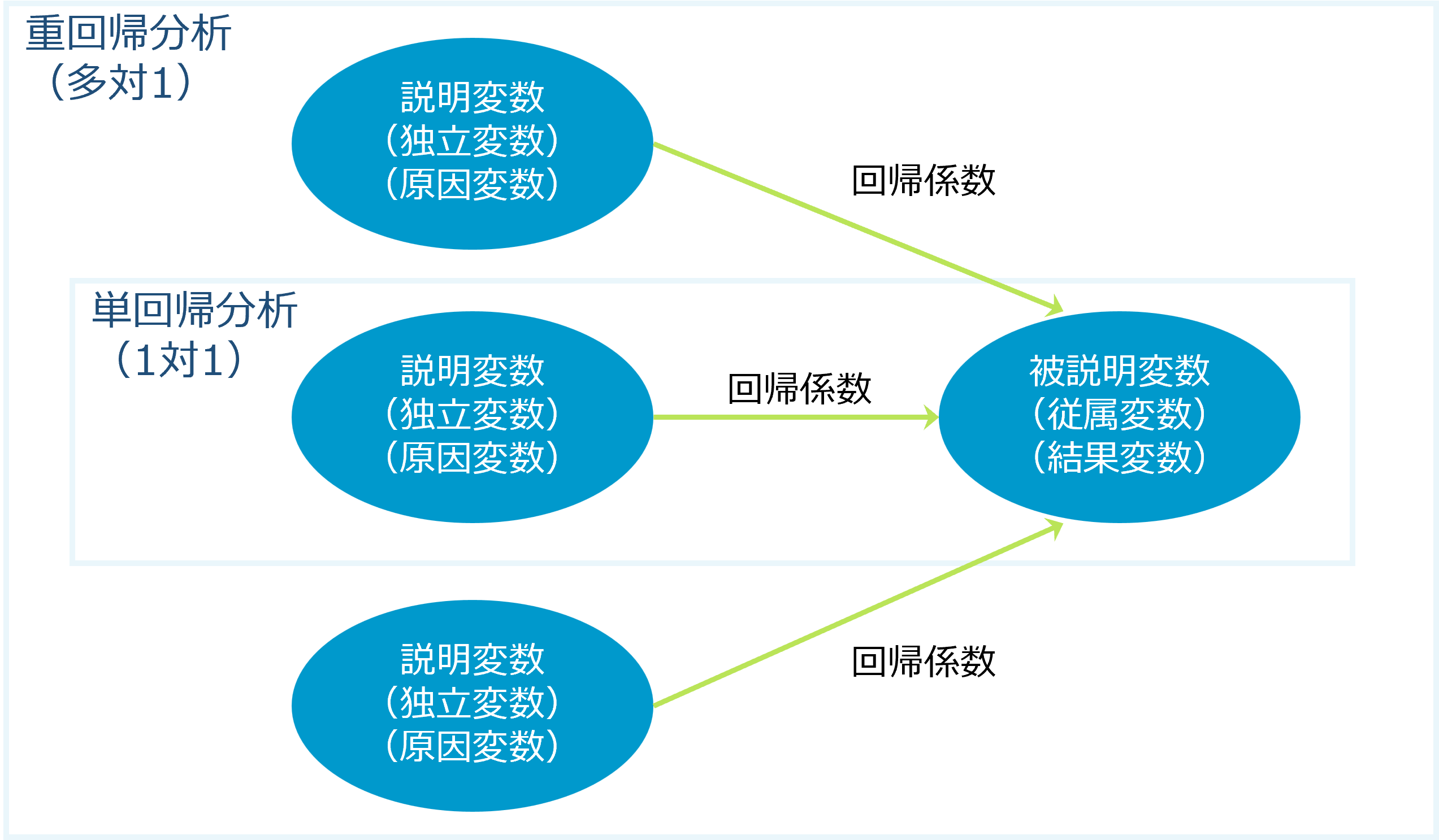
手順1.単回帰分析をする①
前述の相関分析の結果、「口当たり」の数値が上がれば「好意度」はアップ、「軽さ」の数値が上がれば「好意度」はダウンする、という推測も可能です。
もちろん「軽さ」を好むユーザーもいますし、「好意度」と「軽さ」の相関係数の絶対値は0.47と「口当たり」の0.74より低くなっています。
そこで、散布図を使って【「好意度」と「口当たり」】、【「好意度」と「軽さ」】の回帰分析を行ってみましょう。
散布図はExcelで隣り合うセルでしか作成できないため、ローデータのシート内に「好意度」と「口当たり」「軽さ」の行をコピー&ペーストし、散布図の作成元データを作ります。
【「好意度」と「口当たり」】はQ列とR列、【「好意度」と「軽さ」】はT列とU列。
ともに401行目までになります。
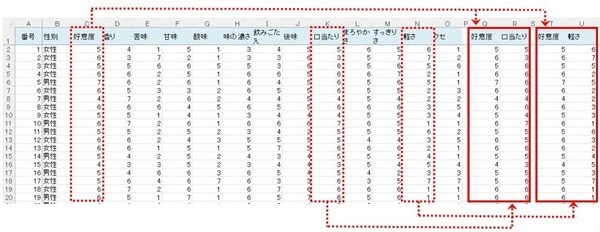
散布図のオプションでは、以下のように選んでください。
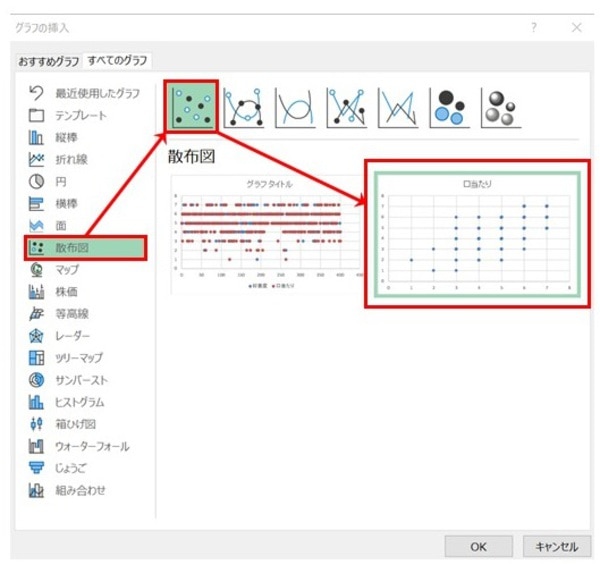
下記のような散布図が作成されました。
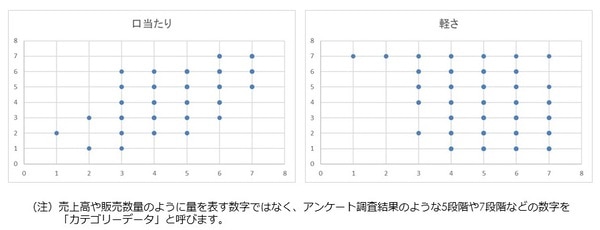
この図から、「口当たり」は「好意度」に対し正の相関、「軽さ」は「好意度」に対し負の相関となることがわかります。
なお、ローデータは好意度、香味特性とも「1~7」のカテゴリーデータ(※)のため、散布図のプロットの数は少なくみえますが、回答者は合計400名なので、多くのプロットが重複しているため、少なく見えています。
※カテゴリデータとは、売上高や販売数量のように量を表す数字ではなく、アンケート調査結果のような5段階や7段階などの数字のことを、カテゴリデータと言います。
手順2.単回帰分析をする②
次に、散布図のグラフエリア内(例えばプロットの上など)にカーソルを置き、右クリックすると、「近似曲線の追加(R)」が表示されます。
クリックすると、右側に「近似曲線の書式設定」が表示されます。
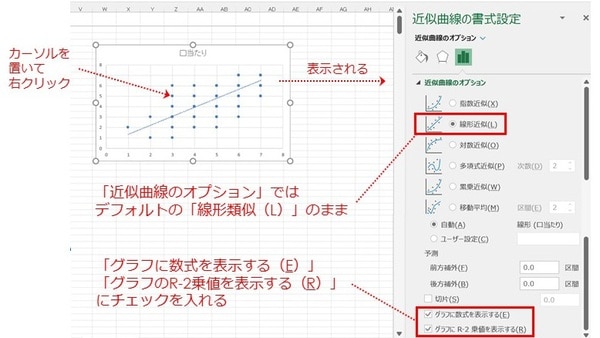
上図の通りに進めると、散布図の右上に数式が入りました。こちらが単回帰式です。
※数式はグラフ上に表示されますので、右上に移動し、タイトルを含め、文字の大きさや太さを調整しています。
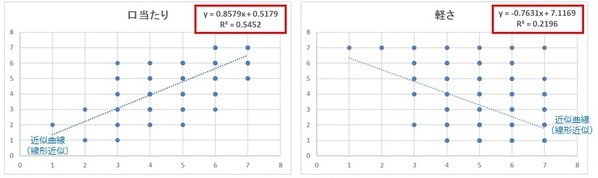
「口当たり」の単回帰式は「y=0.8579x+0.5179」で、 0.8579を「回帰係数(※)」、0.5179を「切片」と呼びます。「口当たり」評価が1だった場合、「好意度」は1.4に、7だった場合は「好意度」6.5になるという計算式です。
※回帰係数とは、回帰分析において、説明変数が目的変数に与える影響の大きさや方向を示す指標です。
「R二乗」は重決定といい、相関係数の二乗です。0から1の数字で、回帰式の当てはまり具合の指標となり、1に近いほうが当てはまりがいいことになります。
もし「R二乗」を1.0と仮定した場合、理論上、 単回帰式の結果はきれいに1から7になるはずですが、 「R二乗」0.54の場合(上記の回帰式は54%説明できる)、「好意度」は1.4~6.5の範囲となります。
【ポイント】単回帰分析結果の見方
当てはまり具合がどの程度良いのか悪いのか? については、経験に基づいた分析者の主観によります。
「相関係数」と同様、その二乗値である「R二乗」(重決定)にも統計的に明確な基準はありません。
後述の「参考:数値データの単回帰分析」で解説しますが、数値データの場合、 「R二乗」(重決定)が0.9以上のように極めて高い数値になることは多々あります。しかし、アンケート調査データの場合は0.9のような高い数値が出ることは多くありません。
実務でも学術でも、対象となる分野やカテゴリーによって各々独自の特徴があります。
よって、「R二乗」(重決定)を絶対的な基準と考えるだけでなく、あるモデルと別のモデルで、どちらの当てはまり具合が良いかなど、相対的に比較するときの基準としても採用されています。
手順3.重回帰分析をする①
Excelで手軽にできるのは「単回帰分析」ですが、その単回帰分析を繰り返すことによって「重回帰分析」を行うことも可能です。
「データ」画面で「データ分析」をクリックすると、「データ分析」のボックスが表示されます。ここで「回帰分析」を選び「OK」をクリックします。
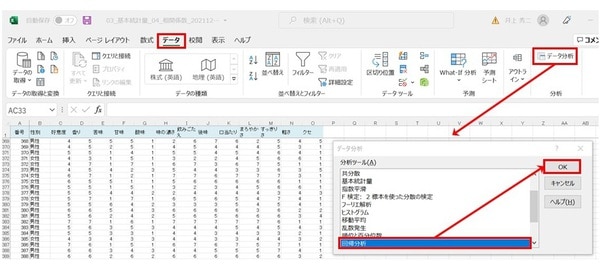
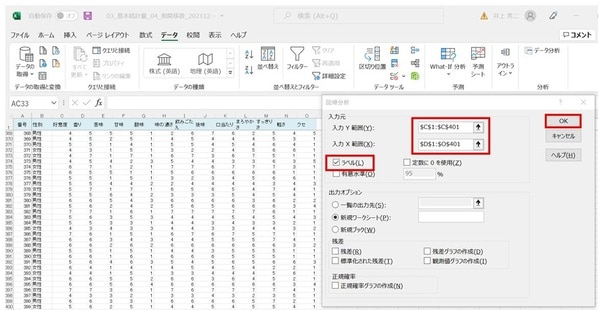
「回帰分析」ボックスでは、「入力Y範囲(Y)」は被説明変数(従属変数)なので、「好意度」(C2からC401)。
「入力X範囲(X)」は説明変数(独立変数)なので、「香味特性(「香り」から「クセ」まで)」(D2からO401)です。
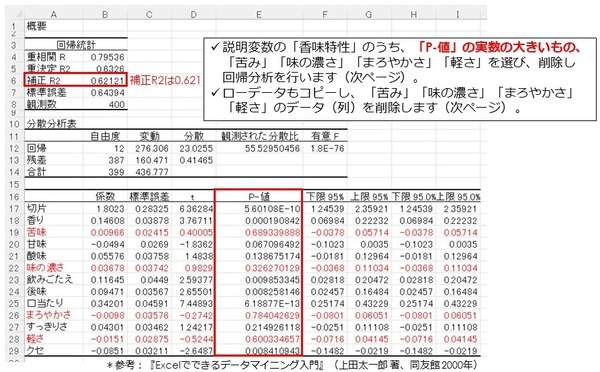
回帰分析結果が、以下のように出力されました。
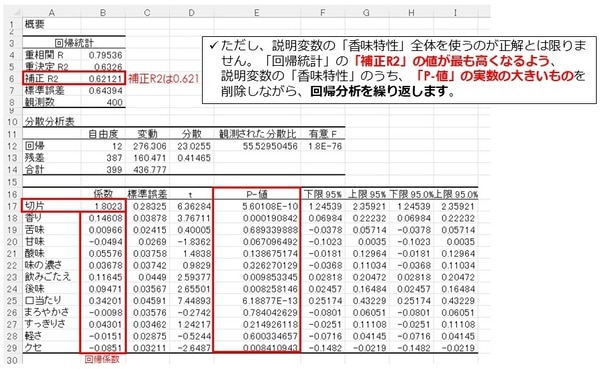
次に「好意度」への影響が相対的に弱い「香味特性」削除の準備をします。
具体的には、説明変数の「香味特性」のうち、「P-値」の実数の大きいもの、「苦み」「味の濃さ」「まろやかさ」「軽さ」を選び、削除し回帰分析を行います。
ローデータもコピーし、 「苦み」「味の濃さ」「まろやかさ」「軽さ」のデータ(列)を削除します。
手順4.重回帰分析をする②
「データ」画面で「データ分析」をクリックすると、「データ分析」のボックスが表示されます。ここで「回帰分析」を選び「OK」をクリックします。
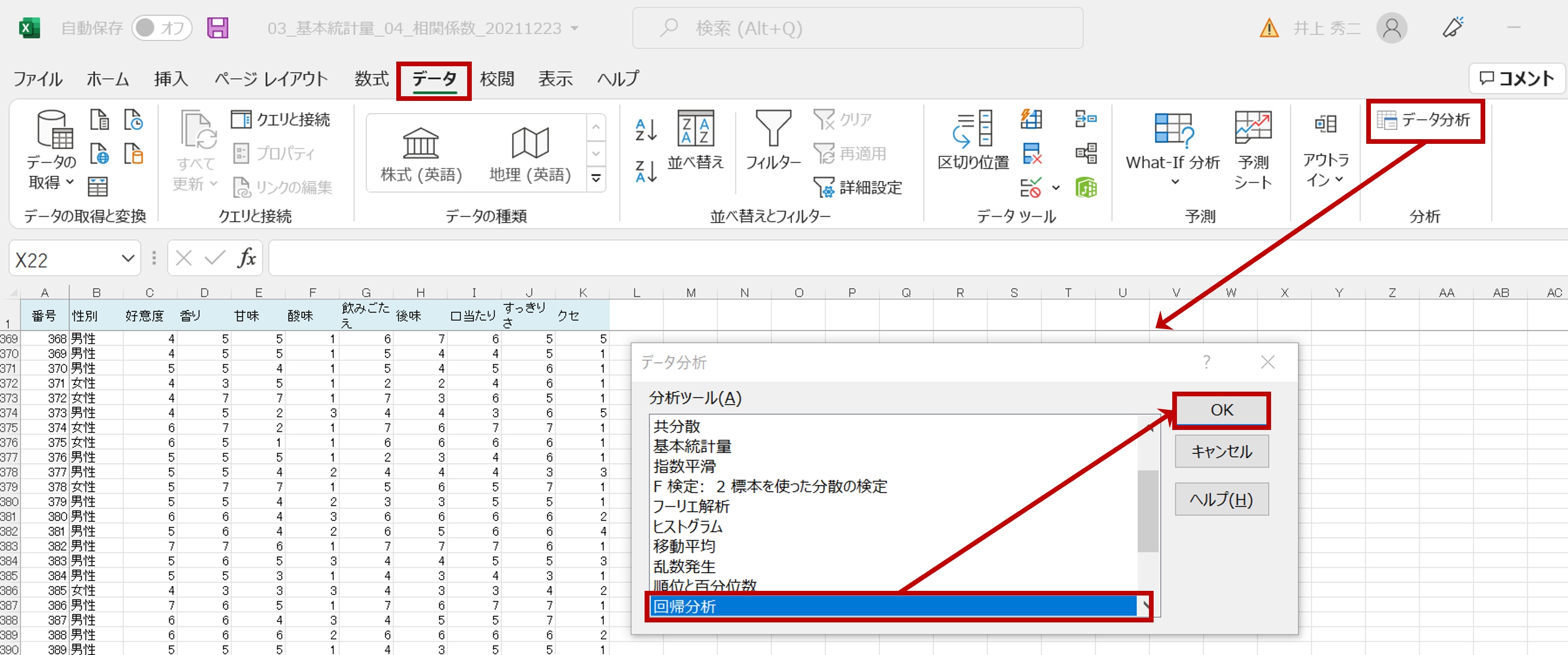
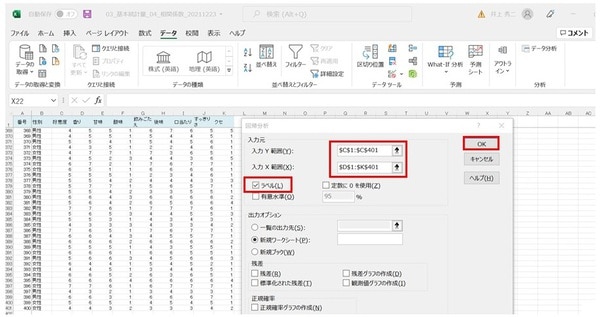
「回帰分析」ボックスでは、「入力Y範囲(Y)」は被説明変数(従属変数)なので、「好意度」(C2からC401)。
「入力X範囲(X)」は説明変数(独立変数)なので、「香味特性(「香り」から「クセ」まで)」(D2からO401)です。
回帰分析結果が出力されました。「補正R2」は0.621から0.624とアップしました。
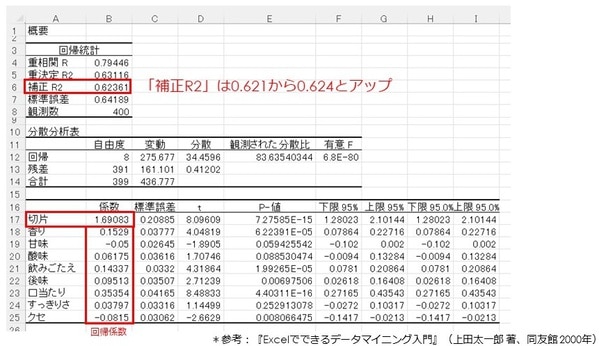
重回帰式は、「切片」に各香味特性の「回帰係数×値」を足し上げていきます。
値はカテゴリーデータの「1~7」の範囲内です。
好意度=1.691+0.153×香り-0.05×甘味+0.062×酸味+0.143×飲みごたえ+0.095×後味+0.354×口当たり+0.038×すっきり-0.082×クセ |
回帰分析は主に予測モデルとして使われます。
今回、アンケート調査結果のカテゴリーデータで重回帰分析を行うメリットは、「香味特性」が「好意度」に与える影響度の測定です。
影響度=回帰係数×データレンジ(範囲) |
データレンジはこのカテゴリーデータの場合、全ての「香味特性」が1から7で同一なので、回帰係数の大きさが「好意度」への影響度ということになります。
つまり「好意度」に最も影響が強いのは「口当たり」(0.35)で、続いて「香り」(0.15)、「飲みごたえ」(0.14)です。逆に「クセ」(0.08)と「甘み」(0.05)はマイナスの影響を与える、ということになります。
数値データ(比率尺度)を使った回帰分析(事例)
ここまで相関分析・回帰分析ともに、アンケート調査結果の「カテゴリーデータ(選択肢の「1~7」など)」を使って実務よりに解説してきましたが、どちらも金額や数量などの数値データ(メトリックデータの比率尺度)によって解説されることのほうが一般的です。
次からは全国の「世帯数」と「新聞発行部数」の関係を事例にして、メトリックデータの比例尺度による回帰分析を解説します。
「世帯数」と「新聞発行部数」の比較
1990年から1997年までの「世帯数と新聞発行部数の推移」データが下記です。
世帯数(千世帯) | 発行部数(千部) | |
1990年 | 41,156 | 51,908 |
1991年 | 41,797 | 52,026 |
1992年 | 42,458 | 51,938 |
1993年 | 43,077 | 52,433 |
1994年 | 43,666 | 52,601 |
1995年 | 44,236 | 52,855 |
1996年 | 44,831 | 53,556 |
1997年 | 45,498 | 53,765 |
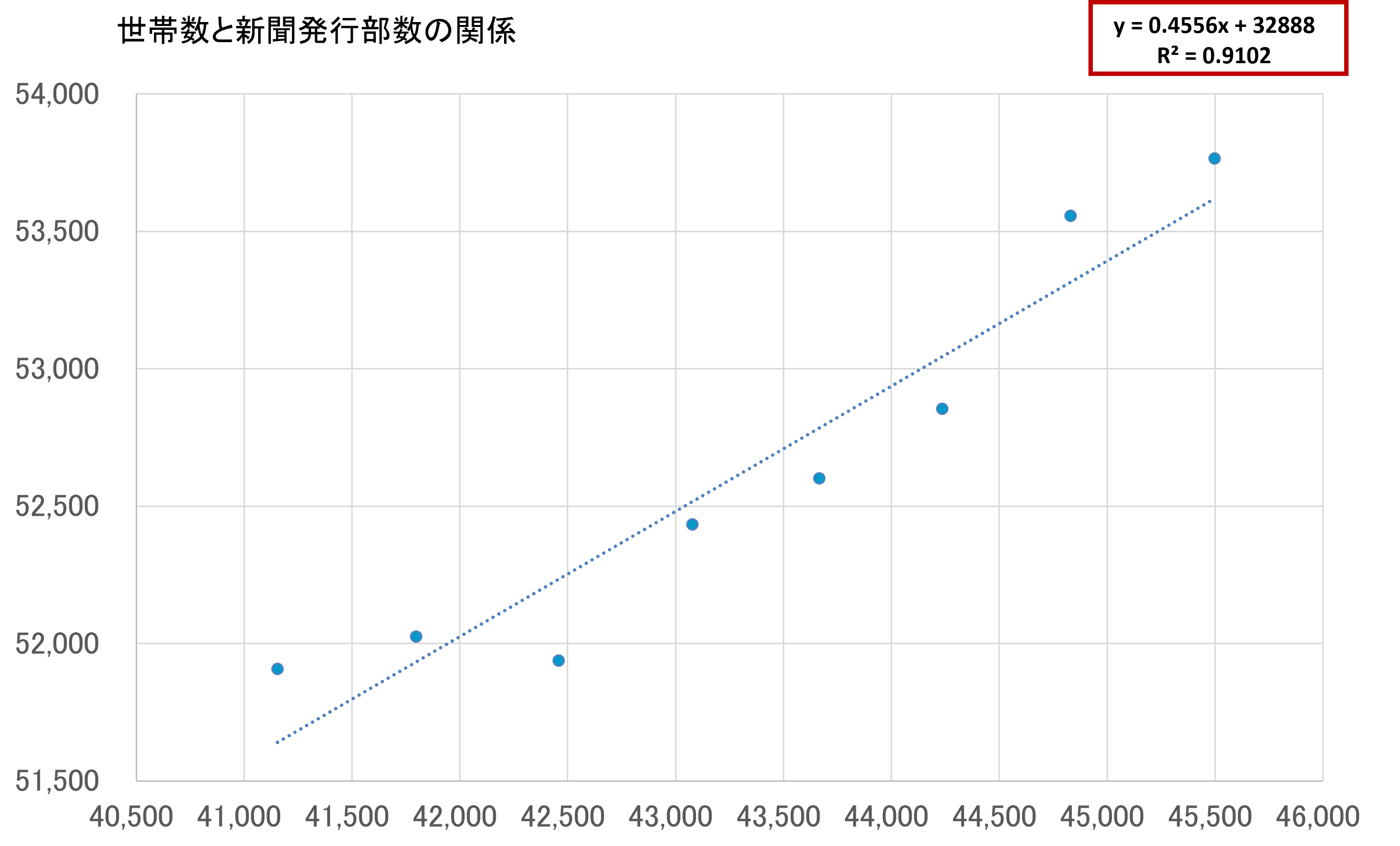
世帯数と新聞発行数の関係が下記です。
2011年から2020年までの「世帯数と新聞発行部数の推移」データが下記です。
世帯数(千世帯) | 発行部数(千部) | |
2011年 | 53,550 | 48,335 |
2012年 | 54,171 | 47,778 |
2013年 | 54,595 | 46,999 |
2014年 | 54,952 | 45,363 |
2015年 | 55,364 | 44,247 |
2016年 | 55,812 | 43,276 |
2017年 | 56,222 | 42,128 |
2018年 | 56,614 | 39,902 |
2019年 | 56,997 | 37,811 |
2020年 | 57,381 | 35,092 |
世帯数と新聞発行部数の関係が下記です。
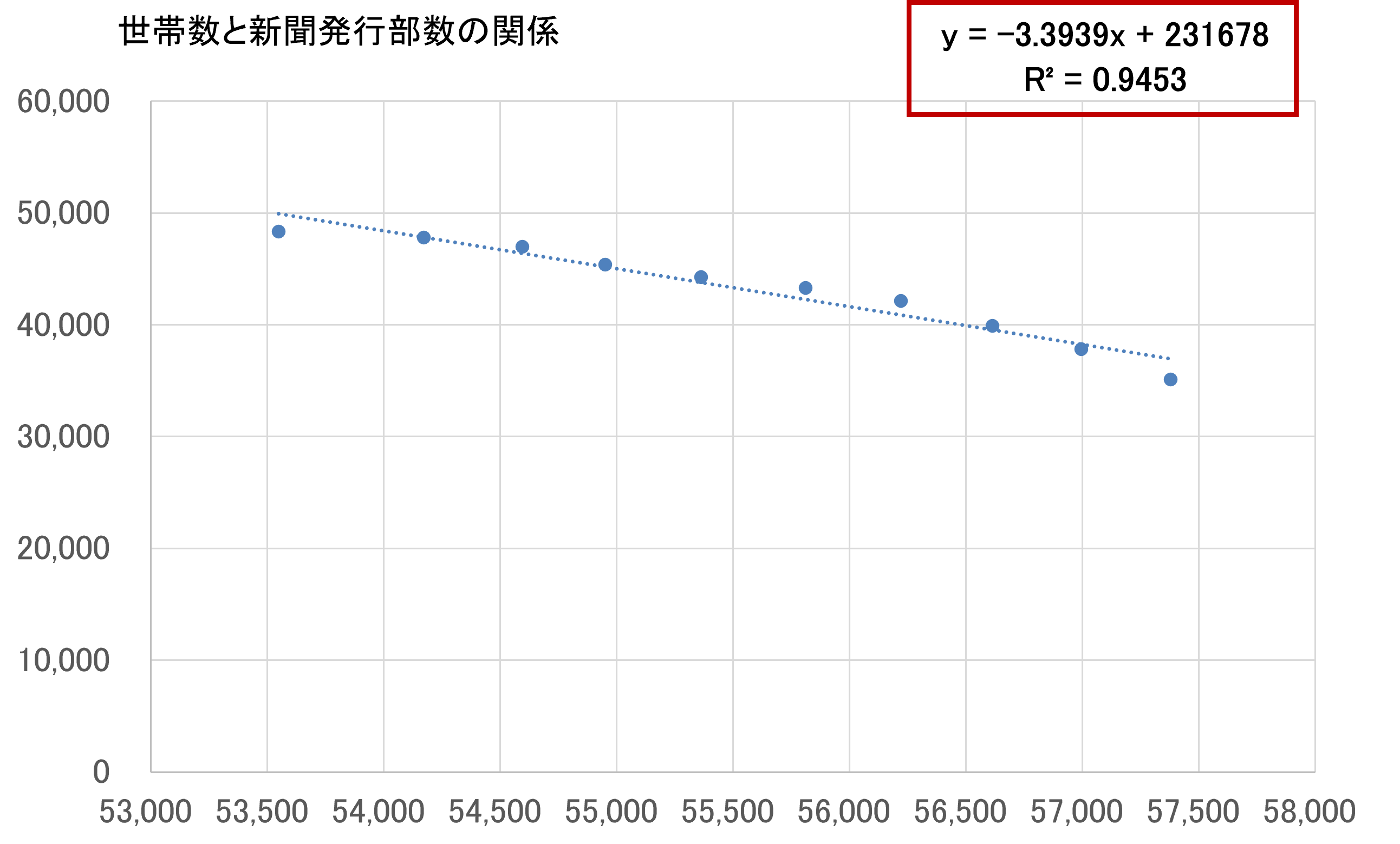
2000年代以前(1990年から1997年までのデータ)、において、「世帯数」と「新聞発行部数」の間には「正の相関」が見られましたが、2010年代以降は「負の相関」です。
少子高齢化と人口減によって、増加している世帯が単身世帯であることに起因するのかもしれません。
どちらも、R2乗は0.910、0.945と、非常に単回帰式の当てはまり具合がいいことが特徴的です。
「世帯数」と「1世帯当たり部数」の比較
続いて、新聞発行部数を「1世帯当たり部数」に変えて回帰分析を行ってみました。
※資料出所「日本新聞協会」サイト
世帯数(千世帯) | 1世帯当たり部数(千部) | |
2011年 | 53,550 | 0.90 |
2012年 | 54,171 | 0.88 |
2013年 | 54,595 | 0.86 |
2014年 | 54,952 | 0.83 |
2015年 | 55,364 | 0.80 |
2016年 | 55,812 | 0.78 |
2017年 | 56,222 | 0.75 |
2018年 | 56,614 | 0.70 |
2019年 | 56,997 | 0.66 |
2020年 | 57,381 | 0.61 |
世帯数と1世帯当たり部数の関係が下記です。
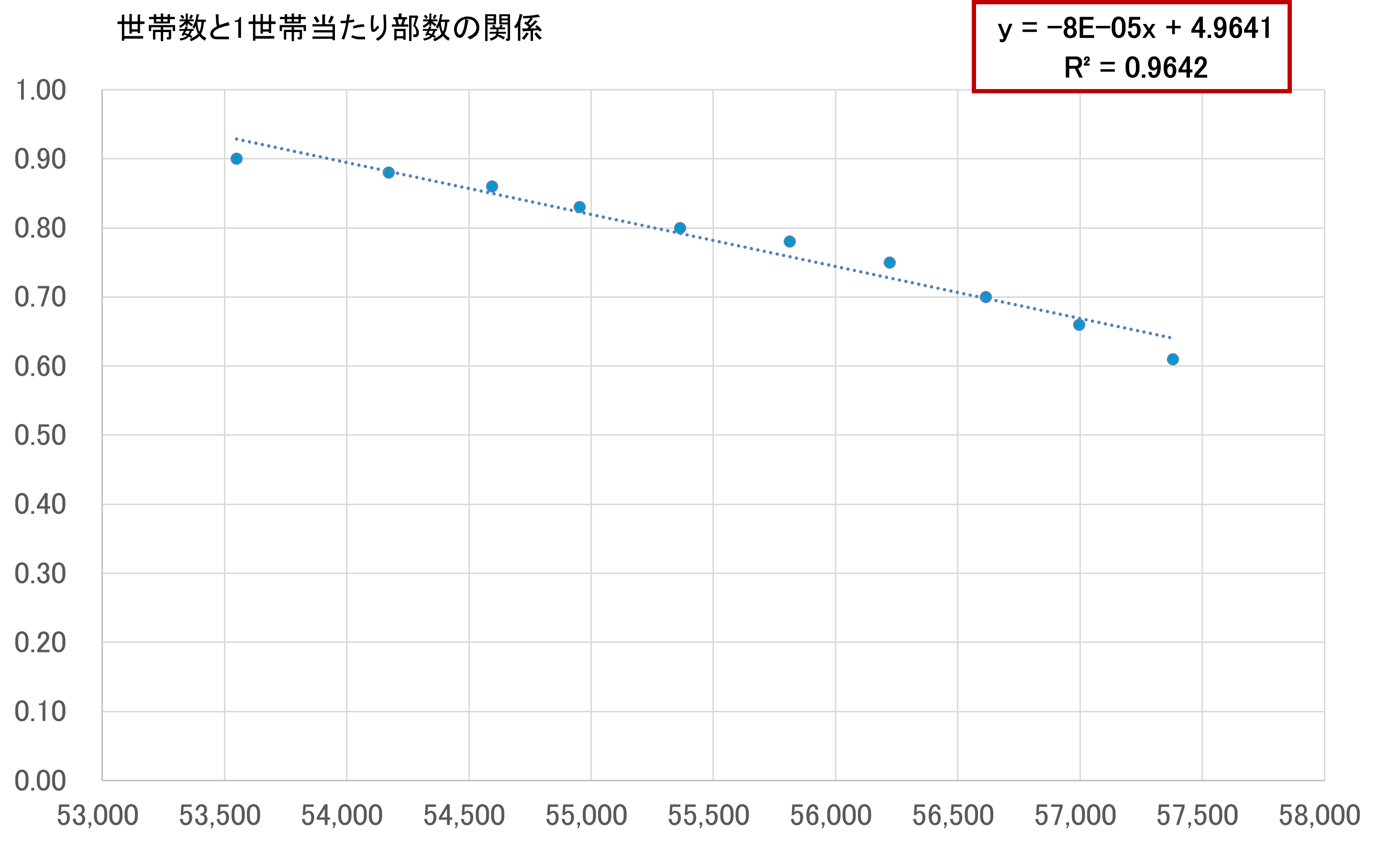
R2乗は0.964と非常に単回帰式の当てはまり具合がいいことがわかります。
「世帯数」は増加しても、「1世帯当たり部数」は逆比例で低下していますので、やはり単身世帯の増加による新聞発行部数の減少という仮説が浮かび上がってきます。
※もちろん、新聞発行部数の減少は、ネットメディアの普及という要因が大きいことは容易に推察されますが、ここではあくまでも世帯数(説明変数)と 新聞発行部数、1世帯当たり部数(被説明変数)との関係を分析しています。
Excelで集計や分析をする際の留意点と次のステップ
ここまでの解説で、「SPSS」や「エクセル統計」などの有償の統計ソフトを使わなくても、Excelを利用したデータの集計や分析がここまでできる!ということをご理解いただけたと思います。
最後に、Excelの集計と分析における留意点と次のステップをまとめました。
正確な分析の第一歩はローデータの管理から
データ分析の基礎はローデータです。ローデータの加工において、関数に誤りがあると、手戻りとなり、時間と労力の多大なロスが発生します。
関数入力後、ドラッグやコピー&ペーストをするとき、絶対参照($)が列だけ必要なのか/行だけ必要なのか/両方とも必要か、を見極めることも、重要です。
また、単純集計表、クロス集計表ともに、あらかじめ作成したフォームに関数を入力する方法が早く正確ですが、もし時間が許すのなら、ピボットテーブルでも集計し、データに誤りがないかを検証すれば万全です。
下記よりダウンロードできる資料内にて、ピボットテーブルでの集計例を解説しているので合わせてご活用ください。
>>📥『ピボットテーブルによる単純集計・クロス集計のやり方』を見る【資料を無料ダウンロード】
相関と回帰分析の関係性を、実務でどう使う?
相関と回帰分析が密接に関係していることは、すでにご理解いただけたかと思います。
実務や学術の現場では、「多対1」の重回帰分析に有償の統計ソフトが使われることが一般的ですが、アンケート調査のカテゴリーデータにおいても、影響度を測る手法として十分に活用できます。
「補正R²」の値が最も高くなるまで回帰分析を繰り返すため、時間と手間はかかりますが、こうした分析手法があることを知っておくことは、決して無駄ではありません。
分析結果を活かすための次のステップ
分析手法を理解した後は、実際にその結果をどう活用するかが重要です。
商品開発や広報など、職種別の活用事例については、以下の記事をご覧ください
資料ダウンロード「エクセルでできるアンケートの集計と分析のやり方」
本記事で解説した「エクセルでできるアンケートの集計と分析のやり方」についてまとめた資料は、下記よりダウンロードすることができます。下記よりダウンロード(無料)して、是非ご活用ください。
おわりに
Excelを使ったアンケートの集計と分析について、必要な知識や具体的な手順を解説してきました。
専門用語が多く、一見難しく感じるかもしれませんが、身近なビジネスツールであるExcelで実践できることを、ぜひ知っておいてください。
日々多くのデータを扱う方々にとって、少しでも役立つ内容であれば幸いです。
【参考文献】
『Excelでできるデータマイニング入門』(上田太一郎 著、同友館 2000年)









