正規分布とは｜リサーチ マーケティング用語集

正規分布

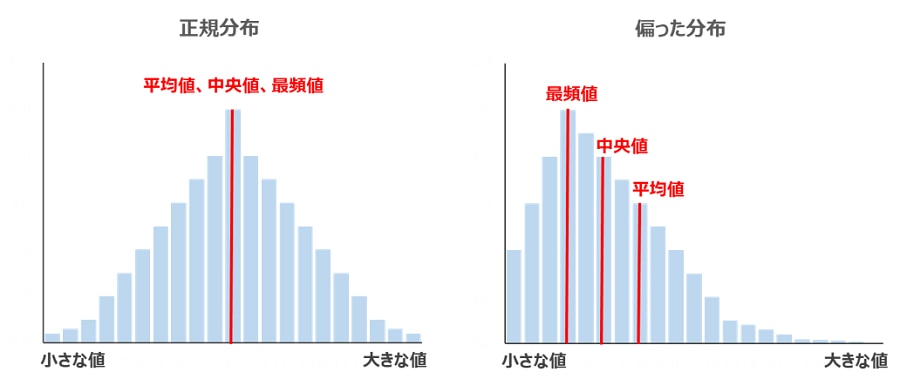
正規分布とは、平均値・最頻値・中央値が一致し、それを軸として左右対称となっている確率分布（※1）です。「ガウス分布」とも呼ばれ、統計学上で最も代表的な分布の一つです。多くの統計的手法は、この正規分布を基礎として展開されており、検定や推定、モデルの作成などの様々な場面で活用されています。

世の中の社会現象や自然現象の中には、その確率変数（※2）が正規分布に従うとみなせるものが、数多く存在します。わかりやすく例を挙げると、人間の身長、テストの点数、サイコロの出目の合計数、雨粒の大きさ、工業製品の規格誤差などが該当します。

一方で、年収や人口、商品の売り上げなど、従うとみなせない現象（正規分布に従わない現象）も存在します。

下図は、正規分布のグラフです。平均を中心に左右対称な曲線で、横軸は「確率変数」、縦軸は「そのときの確率密度」を表します。その形が教会にある釣鐘に似ていることから、「ベルカーブ（bell curve）」とも呼ばれます。

基本的な性質として、分散（標準偏差）が大きくなると、曲線の山は低くなり、左右に広がって平らになります。一方、分散（標準偏差）が小さくなると、山は高くなり、より尖がった形になります。

確率分布とは（※1）

確率分布とは、ある試行で起こり得るすべての事象の確率を出力する関数であり、任意の事象を入力することで、その事象が起こる確率を出力してくれる仕組みのことです。「確率関数」とも呼ばれます。

確率分布の例

【入力値】コインを2回投げて（ある試行）、「表2回が出る」（任意の事象）確率を求めたい → 確率分布（確率関数）の数式で計算 → 【出力値】0.25

確率変数とは（※2）

確率変数とは、色々な値をとる事象が存在しており、それらの値をとる確率が決まっている変数です。

確率変数の例

【入力値】コインを2回投げて、「表2回が出る」確率を求めたい（「表2回が出る」という事象が確率変数です。）

関連用語

平均値 、最頻値、中央値、分散、標準偏差

関連記事

「正規分布」に関連する記事について紹介します。

・平均値の基本知識や関連用語との関係性や違いがわかる！⇒ 『平均値とは？』はこちらから 

・エクセル（Excel）を利用したアンケート集計・分析方法を解説！⇒『アンケート集計と分析の基本』はこちらから