
平均値とは?特徴、求め方、中央値や最頻値との違いを解説!
>>無料ダウンロード【お役立ち資料】平均値の求め方(算出方法)と活用例
目次[非表示]
- ・はじめに
- ・平均値とは
- ・平均値の種類
- ・平均値(算術平均)の注意点、他の代表値(中央値・最頻値)との相違点
- ・代表値の事例(平均値、中央値、最頻値の比較)
- ・代表値同士の関係
- ・Excelで平均値・中央値・最頻値を求める方法
- ・平均値にまつわる、よくある質問
- ・ Q:「分布の中心」を見る代表値(要約統計量) は、平均値・中央値・最頻値の3つだけでしょうか。
- ・ Q:データの「分布の拡がり」とはどのようなイメージのことを言うのでしょうか。
- ・ Q:ここで説明している「加重平均」は、アンケート調査の『選択肢に重みをかけて集計する「加重平均」』とは異なるのでしょうか。
- ・ Q:調査報告書(レポート)において、平均値とともに必ず中央値と最頻値を表示する必要はあるのでしょうか。
- ・ 無料ダウンロード『平均値の求め方(算出方法)と活用例~「代表値」における平均値の位置づけとその種類~』
- ・おわりに(まとめ)
はじめに
ここでは平均値について、基本的な情報や種類、求め方について、事例も交えながら解説していきます。
この記事を読んで分かること、できるようになること
●平均値の意味、基本知識、求め方を習得できる。
●平均値について、関連用語との関係性や違いなどが分かる。
●平均値についてまとめた資料を、無料でダウンロードできる。
平均値とは
平均値とは、データがどのように分布しているか、という特徴を理解する代表値(要約統計量)のうち、最もよく使われる統計値です。平均値には複数の種類がありますが、その中の「算術平均」を指すことがほとんどです。
なお、代表値(要約統計量)は、分布するデータの中心である「平均値」・「中央値」・ 「最頻値」と、分布するデータの拡がり具合である「分散」・「標準偏差」に分けられます。
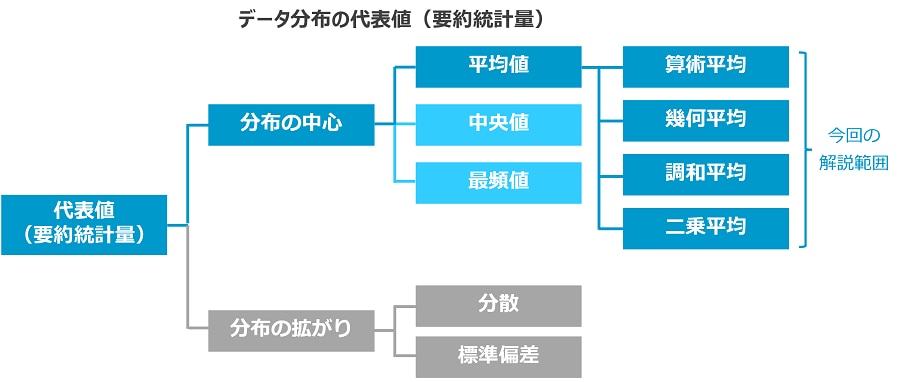
平均値の種類
算術平均
算術平均とは、全てのデータの値を足し合わせた合計を、データの個数で割って算出される平均値のことです。2つの数xとyの算術平均は、『(x+y)÷2』という数式で算出できます。
幾何平均(相乗平均)
幾何平均(きかへいきん)は、比率データ(%)の平均値を算出するときに使われる平均値のことです。相乗平均とも言います。
例えば、ある企業の売上高の伸び率が50%で、次の年に4%減少した場合の、各年ごとの「平均伸び率」を幾何平均で算出してみましょう。
単純に算術平均で計算してしまうと、(1.5+0.96)÷2=1.23、つまり【23%】となります。
もし、1年目の売上高が100万円とした場合、2年目は150万円(50%増)、3年目が144万円(4%減)というのが正確な売上高です。しかし2年目と3年目の伸び率を【算術平均の23%】として計算すると、3年目の売上は151.3万円となり、正確な売上高の144万円を大幅に上回ってしまいます。
よってこの場合は、幾何平均を用いて、2つの数Xとyを掛けてルートにする『√xy』で算出しましょう。
√(1.5×0.96)=√1.44=1.2ですので【20%】になり、つまり2年連続で20%ずつ成長したのと同じ結果となります。3年目の売上高も144万円と正確ですね。
調和平均
調和平均は、移動時の速度などの平均を求める場合に使われる平均値のことです。
例えば、あるマラソン選手が30kmレースで最初の10kmを時速30km、次の10kmを時速25km、最後の10kmを時速10kmで走ったとします。
この場合、30kmが10kmずつ3分割されていますので、算術平均で平均時速を算出すると、【(30km+25km+10km)÷3=21.7km】ということになります。
一方、調和平均により正しく平均時速を求める計算式では、距離の合計を10kmの区間ごとの所要時間の合計で割るため、計算式は【速度=距離÷時間】です。
よって、平均時速=30km÷(10km÷30km+10km÷25km+10km÷10km)=17.3kmとなり、この式で算出した平均時速は17.3kmになります。
この場合の調和平均の計算式は、
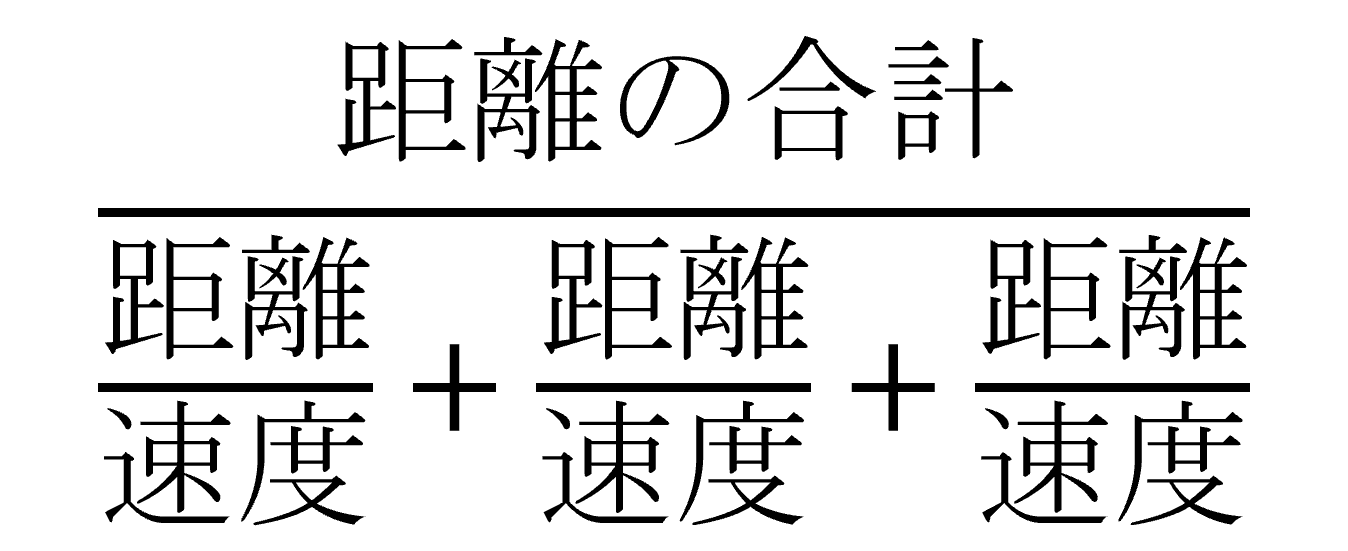
です。下部の分数、
が10kmの区間ごとの所要時間です。
二乗平均
二乗平均は、【正の値(+)】のデータを扱う算術平均と幾何平均(相乗平均)に対して、【負の値(-)】を扱う平均値のことです。「分布の拡がり」をみるために「標準偏差」を算出するときに役立ちます。
どのようなデータでも、偏差の算術平均(偏差の合計÷データ数)は0になってしまう特性があります。プラスのデータとマイナスのデータの相殺を防ぐため、各データを二乗して足して個数で割り、その後にルートにします。
2つの数xとyの二乗平均は、
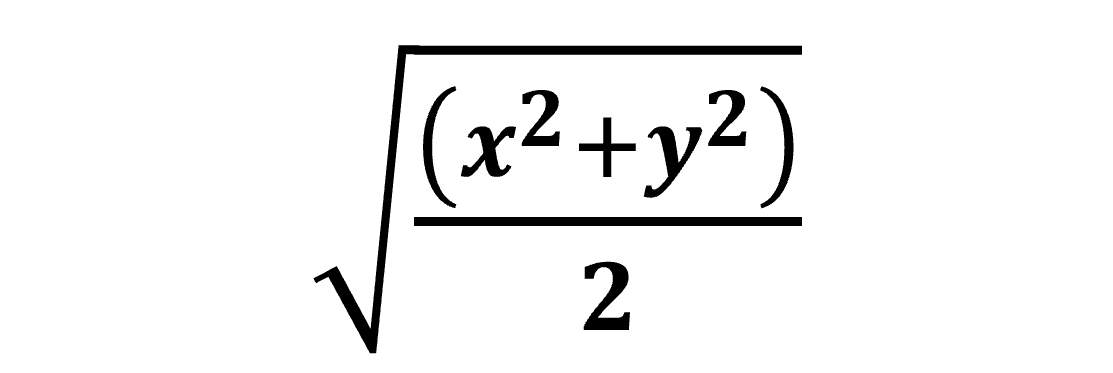
という計算式になります。
加重平均
加重平均とは、算術平均で算出されたそれぞれの値に〝重要度に応じた重み〟を加味して算出される平均値のことです。ここまで紹介してきた代表値(要約統計量)ではありませんが、実務では重視されています。
例えば、売上高が600万円、700万円、800万円の、A・B・Cという3つの商品があるとします。
算術平均で算出した平均売上高は、(600+700+800)÷3=700ですので、700万円ということになります。
もし3つの商品の販売数量が同じだった場合、算術平均の700万円で問題ありませんが、販売数量が各々、100個・100個・200個だった場合、販売数量の〝重み〟を加味した加重平均を使います。
販売数量の合計は400個です。 A・B・Cのそれぞれの数量構成比は、25%・25%・50%です。
A・B・Cの各売上高の600万円・700万円・800万円のそれぞれに、数量構成比25%・25%・50%を掛け合わせると、150万円・175万円・400万円となります。この3つの金額を足し合わせた加重平均値は725万円です。
加重平均値の725万円が算術平均の700万円より25万円高くなったのは、売上高・数量構成比ともに最も高いC商品の〝重み〟が加味された結果です。
平均値(算術平均)の注意点、他の代表値(中央値・最頻値)との相違点
平均値において最も注意しなければならない点として、「外れ値」による影響を受けてしまう点があります。
「外れ値」とは、値が極端に大きいデータや、極端に小さいデータのことです。この外れ値により、平均値は大きいか小さいほうに引っ張られてしまうため、適切に扱わないと、データを分析した際の結果に大きな歪みが生じる可能性があります。
そこで、「外れ値」の影響を受けにくい他の代表値である「中央値」と「最頻値」も算出することが大切です。
中央値
中央値とは、データを値の小さい順から並べて、中央に位置する値のことです。中央にあたるデータが奇数個の場合はその値を中央値とし、偶数個の場合は2つの値の算術平均で算出します。
最頻値
最頻値とは、データの中で最もデータの個数(登場頻度)の多い値のことです。
3つの代表値のまとめ(特徴、メリット、デメリット)
平均値(算術平均)、中央値、最頻値の3つの詳細を分かりやすく表にまとめました。
代表値 | 特徴 | メリット | デメリット |
平均値 | 平均値のうち最もよく使われる「算術平均」は、データの値を合算し個数で割った値 | 全てのデータを考慮できる | 外れ値の影響を受けやすい |
中央値 | データを値の小さい順から並べて、中央に位置する値 | 外れ値の影響を受けにくい | 全てのデータを考慮できない |
最頻値 | データの中で最もデータの個数(登場頻度)の多い値 | 外れ値の影響を受けにくい | データの個数が多い場合にしか使えない |
代表値の事例(平均値、中央値、最頻値の比較)
ある事例を使い3つの代表値を比較して、実際に「外れ値」による影響を受けるとどのようなデータになるかを見てみましょう。
下のグラフは、厚生労働省の「2021年国民生活基礎調査」による所得金額階級別世帯数の割合です。各代表値を算出すると、平均値が564万3千円で最も高く、中央値が440万円、グラフには表示されていませんが最頻値は300万円以上400万円未満の値であることが分かります。
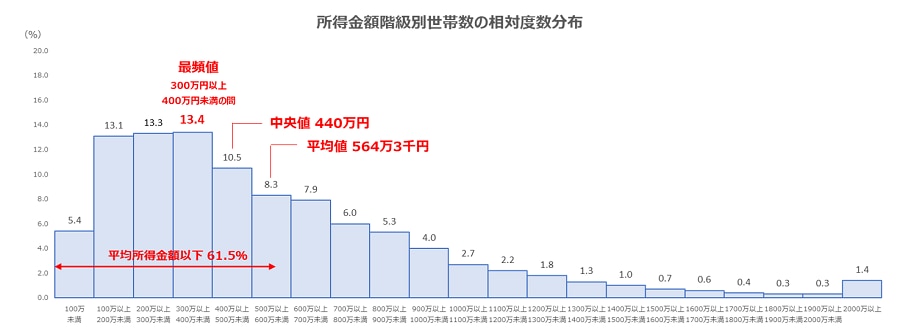
↓【上記の左部分だけを拡大した画像】
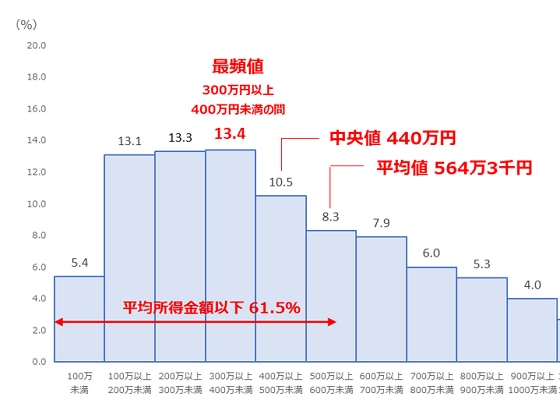
平均値が最も高いのは、グラフの最も右側の「2000万円以上」という所得金額の高い層の1.4%に引っ張られているからです。そのため、平均所得金額以下の世帯が全世帯の6割強(61.5%)を占める結果となってしまいました。
代表値同士の関係
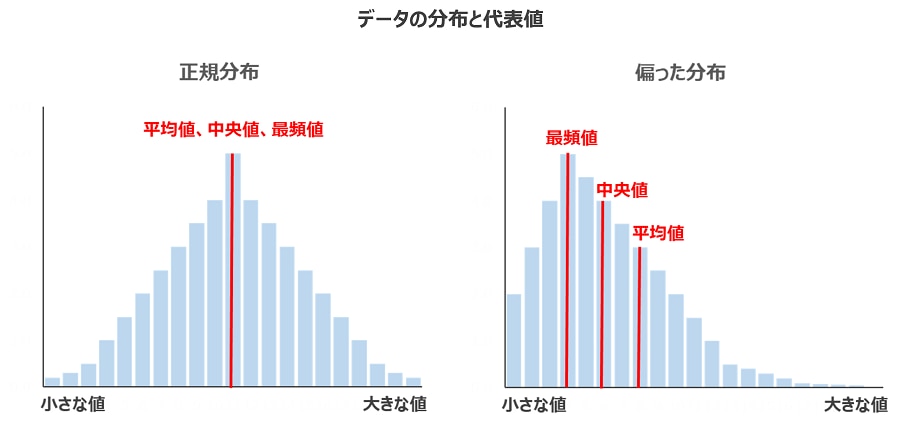
データの分布と、3つの代表値(平均値・中央値・最頻値)の関係をグラフに表すと、下記のようになります。
正規分布では、3つの代表値は同一となります(左のグラフ)。一方、先述の事例「所得金額階級別世帯数」の割合と同様、小さな値の側にデータの分布が偏っている場合、最頻値・中央値・平均値の順に値が高くなります(右のグラフ)。
Excelで平均値・中央値・最頻値を求める方法
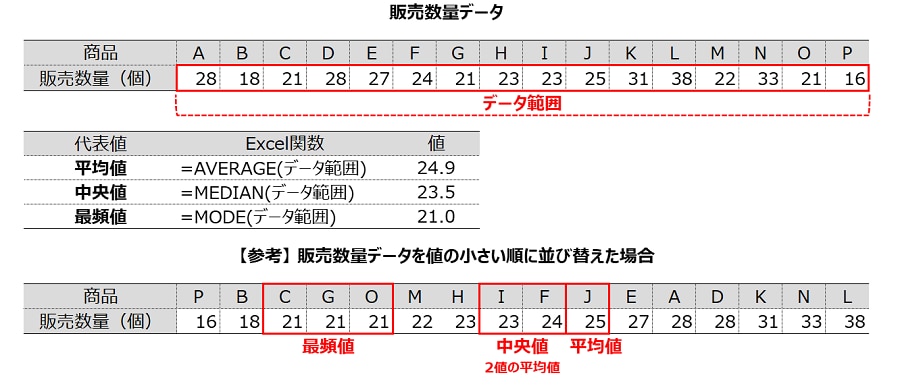
平均値(算術平均)、中央値、最頻値の3つの代表値は、Excelの関数で簡単に算出することができます。
関数はそれぞれ、【平均値:AVERAGE】、【中央値:MEDIAN】、【最頻値:MODE】です。
平均値にまつわる、よくある質問
Q:「分布の中心」を見る代表値(要約統計量) は、平均値・中央値・最頻値の3つだけでしょうか。
厳密には「最小値」と「最大値」を含めることもあります。平均値(算術平均)は「外れ値」の影響を受けてしまうため、データの中の最も小さい値と最も大きい値を明記しておいた方が、どの程度の「外れ値」があるかが分かるというメリットがあります。
しかしながら、実務上ではほとんど必須とされていません。
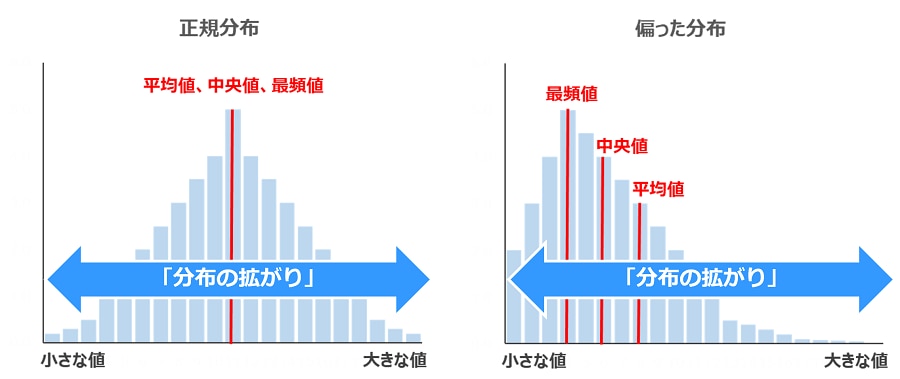
Q:データの「分布の拡がり」とはどのようなイメージのことを言うのでしょうか。
データの「分布の拡がり」とは「最小値」から「最大値」までの『データの拡がり具合』のことで、具体的な数値が「分散」と「標準偏差」です。
Q:ここで説明している「加重平均」は、アンケート調査の『選択肢に重みをかけて集計する「加重平均」』とは異なるのでしょうか。
異なります。後者のアンケート調査の『選択肢に重みをかけて集計する「加重平均」』では、5段階評価の場合、「とても好き=2」「まあ好き=1」「どちらともいえない=0」「あまり好きではない=-1」「とても嫌い=-2」、という重みをかけます。
前者の「加重平均」(売上高に販売構成比の重みを掛け合わせたケース)とは異なります。
Q:調査報告書(レポート)において、平均値とともに必ず中央値と最頻値を表示する必要はあるのでしょうか。
学術調査の場合は、基本統計量を全て表示することが多いですが、実務の調査報告書(レポート)、特に生活者対象の定量調査の場合、中央値と最頻値を表示するケースは必ずしも多くはありません。企業の意思決定に資するレポートにおいては、具体的で、意思決定に直接影響する数値のみが重要視されるためです。
統計的な正確性が求められる場合、「偏った分布」のローデータ全てを標準化する、つまり「正規分布(平均値・中央値・最頻値が等しい) 」のデータに変換してから、集計・分析をするケースもあります。
無料ダウンロード『平均値の求め方(算出方法)と活用例~「代表値」における平均値の位置づけとその種類~』
本記事で解説した内容をまとめた資料「平均値の求め方(算出方法)と活用例~「代表値」における平均値の位置づけとその種類~」は、下記よりダウンロードすることができます(無料)。
おわりに(まとめ)
最後に、ここまで解説してきた内容をまとめました。復習としてご活用ください。
●「代表値」のうち、最もポピュラーなものが「平均値」である
データがどのように分布しているかという特徴を理解するための「代表値」のうち、データの「分布の中心となる値」には、平均値・中央値・最頻値の3つがあります。
また、平均値には、算術平均・幾何平均(相乗平均)・調和平均・二乗平均の4種類があります。
一般的には、平均=算術平均(全てのデータを加算して、データの個数で割って算出する)を指すことがほとんどです。
・幾何平均(相乗平均)は、伸び率などの比率データ(%)の平均値を求める場合に使います。
・調和平均は、移動時の速度などの平均を求める場合に使います。
・二乗平均は、データの「分布の拡がり」を求める代表値、具体的には標準偏差を算出する際に使います。
なお、「代表値」としての平均値ではありませんが、金額に対して数量の〝重み〟を加味するような加重平均も使われます。
●平均値を算出する際は、中央値・最頻値も算出する
平均値(算術平均)のデメリットは、外れ値(異常に小さいか大きい値)に引っ張られてしまうことです。そのデメリットを補うために、中央値(データを値の小さい順から並べて、中央に位置する値)と最頻値(データの中で最もデータの個数=登場頻度の多い値)も算出します。
なお、Excelでは、【平均値:AVERAGE】、【中央値:MEDIAN】、【最頻値:MODE】という関数で、簡単に算出することができます。
【参考文献】
『マーケティング・リサーチの基本』(岸川茂編著、JMRX著、日本実業出版社、2016年10月)/『完全独習 統計学入門』(小島寛之著、ダイヤモンド社、2006年9月)/『ウルトラ・ビギナーのためのSPSSによる統計解析入門』(小田利勝著、プレアデス出版、2007年6月)/『電通現役戦略プランナーのヒットをつくる「調べ方」の教科書』(阿佐見綾香著、PHP研究所、2021年10月)






