サンプルサイズとは？基本と計算方法を簡単解説！

はじめに

アンケート調査に欠かせない「サンプルサイズ」。ここでは、その基本的な意味から、似ている言葉の「サンプル数」との違い、さらに関わりが深い「出現率」について、分かりやすく解説していきます。

1.サンプリングプロセス

サンプリングプロセスとは

サンプリングプロセスとは、①母集団の定義から始まり、②サンプリングフレームの決定、③サンプリング方法の決定、④サンプルサイズの決定（本ブログでのテーマ）、⑤サンプリングの実行というステップです。

母集団とサンプル（標本）

サンプルサイズの詳しい説明に入る前に、理解しておくべき4つの統計用語、「母集団（N）」
「母集団のサイズ」「サンプル（標本）（n）」「サンプルサイズ」について説明します。

【4つの統計用語】

母集団（N）

調査の対象となる集団の全体

母集団のサイズ

母集団の大きさのことで、データの個数。個数は「N=数字」として表現する

サンプル（標本）（n）

母集団の一部から抽出して（抜き出して）作ったサンプル（標本）の集団

サンプルサイズ

母集団の一部から抽出したサンプル（標本）の個数。個数は「n=数字」として表現する

例えば調査対象者が「東京都在住の20代女性」の場合、「東京都在住の20代女性の全体」が「母集団」となります。その母集団の「データの個体数」を「母集団のサイズ」（母集団の大きさ）といいます。
ここでは母集団のサイズは89万9,000人なので（総務省統計局人口推計 2019年10月1日確定値より） 、N=899,000と表します。
しかし、 89万9,000人全員を対象に調査することは現実的ではありません。

そこで「東京都在住の20代女性」89万9,000人の「母集団」の中から、例えば200人を無作為に抜き出した「サンプル（標本）」という集団を作って調査を行い、母集団全体における傾向を推測します。この場合、サンプルサイズ＝200人（n=200）となります。

​​​​​​​

2. サンプルサイズとサンプル数

サンプルサイズとは

サンプルサイズとは、母集団から抽出したサンプル（標本）のデータの個数のことです。
前項の例の続きで解説しますと、ここでは、サンプルサイズ＝200人（n=200）となります。

このように統計学では、「母集団」と「サンプル（標本）」を明確に区分します。
そして、母集団のサイズ（大きさ）を表すときには大文字の「N（ラージエヌ）」、サンプルサイズを表すときは小文字の「n（スモールエヌ）」と使い分けます。

母集団の一部を抽出して行う調査を「標本調査」（サンプリング）というのに対して、母集団全体を対象とする調査を「全数調査」（センサス）といいます。
代表的な全数調査は、日本に住んでいる人全員を対象とした「国勢調査」、日本国内の全ての事業所・企業を対象とした「経済センサス」です。

サンプル数とは

サンプルサイズと似た言葉に「サンプル数」がありますが、同義語ではありません。

サンプル数とは、サンプルの抽出を行った回数であり、サンプル（標本）集団の数のことです。
「東京都在住の20代女性」89万9,000人の「母集団」の中から、例えば200人を無作為に抜き出した場合、サンプル数は1、ということになります。

さらに200人ずつの抽出を繰り返していった場合、サンプル数は1つずつ増えることになります。

>>「サンプル数の分かりやすい図解」を見る【資料を無料ダウンロード】

サンプルサイズの計算式

サンプルサイズを決めるためには、以下の3つの統計情報が必要となります。

① 標準偏差（S）

標準偏差とは、母集団の異質性を示す分散から平方根をとった数値です。
母集団の要素が均一であれば（標準偏差が小さい場合）、サンプルサイズは小さくてもいいですが、異質であれば（標準偏差が大きい場合）、サンプルサイズは大きくする必要があります。

② 誤差の許容範囲（E）

誤差の許容範囲とは、母集団とサンプルの誤差をどの程度まで許せるのか？ということです。
簡単な意思決定ならば誤差はある程度許され、サンプルサイズは小さくてもよいですが、重要な意思決定ならば誤差には厳しくなるので、サンプルサイズは大きくする必要があります。

③ 信頼水準（Z）

信頼水準は、90％、95％、99％のいずれかが適用され、通常95％が使用されます。 信頼水準95％の場合とは、サンプルから推計される母集団の平均値が誤って推定される確率が5％ということです。

これら3つの数値を使った、単純無作為サンプリングにおけるサンプルサイズ（n）は、以下の計算式で算出することができます。

>>【関連記事】無料計算ツールあり！必要なサンプルサイズを計算したい方はこちらの記事へ

分析軸によるサンプルサイズの検討

ここまではサンプルサイズの計算式を紹介しましたが、ほとんどの調査では母集団の平均値や分散、標準偏差は事前にわかりません。よってここでは、調査設計過程でサンプルサイズを決める方法を紹介します。

サンプルサイズは「必要となる分析軸」から逆算して決めていきます。「分析軸」とは、調査結果のデータ（数値）を集めて集計した「集計表」の表側にある「性別」「年齢別」「地域別」のような「分析の視点」を並べたもののことです。

「セルごとの人数」は統計上、分析に耐えられるだけの数（30人）が必要なので、必要な人数から
回答を得られるかということが重要になります（30人未満の場合は「参考値」ということになります）。

ただし30人は分析可能なギリギリの人数ですので、1セル50人を目安にしたほうが安全です。その結果、サンプルサイズ（合計）は400人となりました。（以下、「3. 出現率調査」に続きます）

>>「サンプルサイズのマニュアル」をダウンロードして読む【資料を無料ダウンロード】

3. 出現率調査

出現率とは

1つのセルで50人以上確保したい場合、全体のサンプルサイズは400人でした（前項から続く）。
次に「自社のハンドクリーム商品Aをすでに購入した20～30代」を「分析軸」として使いたい場合を考えます。

このハンドクリーム商品Aは、まだ発売から1年しか経っておらず認知も不十分なため、「何らかのハンドクリームの年1回以上購入者」の中でも購入者は極めて少ないと想定されます。

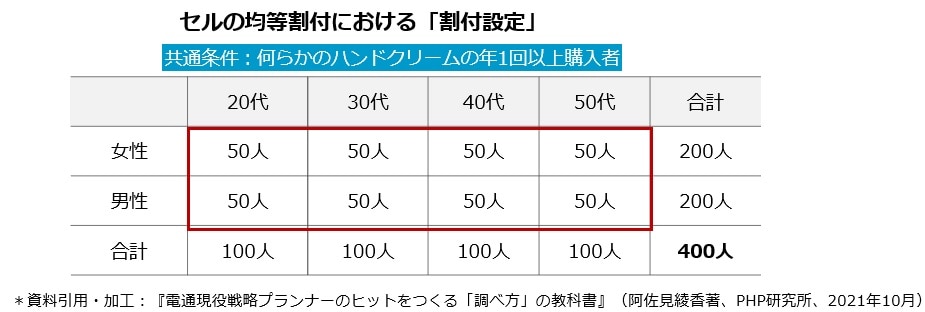
「サンプルサイズの決定（分析軸による検討）」で割付した設計では、20～30代は合計200人確保できる設計でした（下表赤線囲み内）。その200人の中で「ハンドクリーム商品Aの購入者」がもし15％いれば、購入者は30人、非購入者は170人ということになります。

この場合、購入者30人がギリギリ確保できそうなので、集計はかろうじて可能といったところです（しかも女性・男性の性別ごとの集計は不可能）。この15％という数字を「出現率」といいます（出現率＝割付の条件該当者数÷母集団の人数）。

出現率によるサンプルサイズの調整

前項では、出現率15％、サンプルサイズ400人としましたが、それでも各セルでの分析はギリギリの人数で行わねばなりません。さらにもし出現率が10%しかなかった場合、どうすればいいでしょうか。

出現率10％の場合、 200人のうち20人しか出現しないので分析軸として成立しないことになります。そして、最も人数が少なくなりそうな分析軸に合わせて、サンプルサイズを大きくすることが解決策となります。

出現率によるサンプルサイズの調整方法や、最も数が少なそうな分析軸のセルの部分だけの「ブーストサンプル」調整について、具体例を交えた資料をご用意しています。下記よりダウンロードしてご覧ください。

>>「出現率によるサンプルサイズの調整方法や例」を見る【資料を無料ダウンロード】

4. サンプルサイズにまつわる、よくある質問

Ｑ：サンプル数とは、標本抽出の回数とのことですが、回数が多くなるのはどのようなケースでしょうか？

例えば全国47都道府県での傾向を比較したい場合、47都道府県から無作為抽出をします。その場合、「サンプル数は47」ということになります。

Ｑ：サンプルサイズを計算式で算出することは少ないのでしょうか？

実際のところほとんどの調査では設計段階で、母集団の平均値や分散、標準偏差が不明であるばかりではなく、母集団のサイズ（データの個体数）さえ推定できないケースがほとんどです。となると計算式はあっても実際には使えません。よって、分析軸によるサンプルサイズの検討・調整を行うほうが現実的です。

>>サンプルサイズに関するQ&Aをもっと見る【資料を無料ダウンロード】

おわりに

ここまでサンプルサイズに関する基本的な知識、活用方法を、具体例とともに解説してきました。
実際にアンケート調査を実施する時は、より実践的な内容となっている別記事「サンプル数の決め方」もぜひご活用ください。

>>【関連記事】無料計算ツールあり！必要なサンプルサイズが分かる！ブログ「サンプル数の決め方」はこちら

無料ダウンロード「サンプルサイズのマニュアル～サンプルサイズ・サンプル数・出現率とは～」

本記事で解説した「サンプルサイズ」についてまとめた資料は、下記よりダウンロードすることができます（無料）。
こちらの資料では、記事では紹介できなかった、出現率によるサンプルサイズの調整方法や、「ブーストサンプル」調整、よくある質問等を掲載しています。
無料ですので、下記よりダウンロードしてご活用いただけますと幸いです。