Excelで分散分析(ANOVA)を行う方法|一元配置・二元配置の基本と実践手順を解説
はじめに|Excelで分散分析を理解・実践するために
Excelで分散分析(ANOVA)を行いたいけれど、「一元配置と二元配置の違いが分からない」「P値や分散比の見方に自信がない」そんな悩みをお持ちではありませんか。
本記事では、分散分析(ANOVA)の基本概念から、因子・水準・仮説と対立仮説の考え方、そしてExcelの分析ツールを使った具体的な手順までを、実際のデータ例と画像付きで分かりやすく解説します。
一元配置分散分析・二元配置分散分析(繰り返しあり/なし)それぞれについて、Excel上での操作方法と結果の読み取り方を丁寧に説明しているため、統計が苦手な方でも、実務で分散分析を使えるようになる内容です。
記事の最後では、内容をまとめた無料資料「分散分析マニュアル(Excel対応)」もダウンロードできますので、ぜひ実務や学習にお役立てください。
この記事を読んで分かること、できるようになること
- 分散分析の基本概念と用語の理解
- Excelを使った分散分析の具体的なやり方の習得
- 分散分析マニュアル(無料資料)のダウンロード
分散分析(ANOVA)とは
分散分析の概要と目的
分散分析(ANOVA:Analysis of Variance)とは、3つ以上のデータがある場合、それぞれの平均値の間に有意な差があるのかないのか、そして差があるとすれば、どの平均値とどの平均値の間に差があるのかを判定する手法(有意差の検定)です。
分散分析が使われる分野
広い意味では製造業などの品質管理でよく用いられる実験計画法に含まれますが、分散分析としてマーケティングリサーチ分野で広く活用されています。
分散分析の基本概念
分散分析を理解するためには、まず基本となる用語と、分散分析の種類を整理して押さえておくことが重要です。ここでは、因子・水準・一元配置法といった用語の意味と、分散分析の代表的な種類について解説します。
因子・水準・一元配置法とは
下表は、あるスーパーマーケットが「特売情報の折込チラシ」を、4種類の新聞に3回入れて、どの新聞への折り込みチラシが来店の効果があったのかを調査した例です。
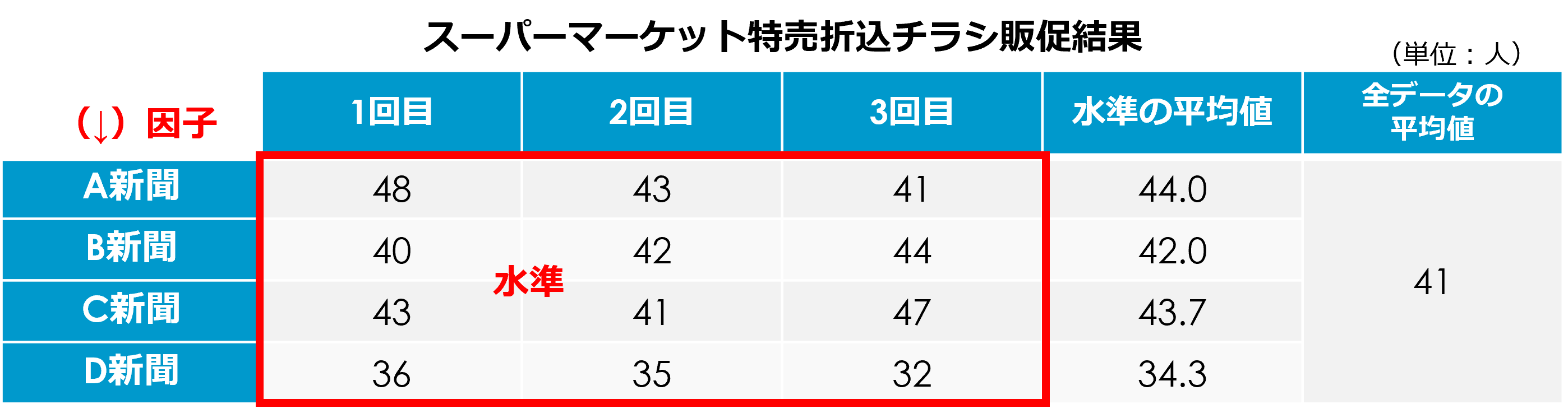 この調査において、因子とは結果に影響を与える一つの要素のことで、ここでは「新聞」が因子にあたります。
この調査において、因子とは結果に影響を与える一つの要素のことで、ここでは「新聞」が因子にあたります。
このような一つの因子の影響だけを分析する分散分析のことを「一元配置法」と呼びます。
また、A新聞・B新聞・C新聞・D新聞ごとに得られた一つ一つの観測データのことを、水準といいます。
分散分析では、これらの水準ごとのデータをもとに、平均値に差があるかどうかを検定します。
分散分析の種類
分散分析には、主に次の3つの種類があります。
因子が一つか二つか、また因子が二つの場合は、各因子の組み合わせごとに複数のデータ(繰り返し)がある場合と、一つのデータしかない(繰り返しがない)場合に分かれます。
一元配置分散分析
一つの因子の影響を分析する方法です。
二元配置分散分析(繰り返しあり)
二つの因子とその交互作用を詳細に分析する(同じ条件のデータが複数ある)。
二元配置分散分析(繰り返しなし)
二つの因子の影響を分析する(同じ条件のデータが一つしかない)。
分散分析の仕組みを理解する
水準内変動(実験誤差)とは
先述したスーパーマーケットの事例の調査目的は、どの新聞の折込チラシに来店効果があったかどうかの検証です。
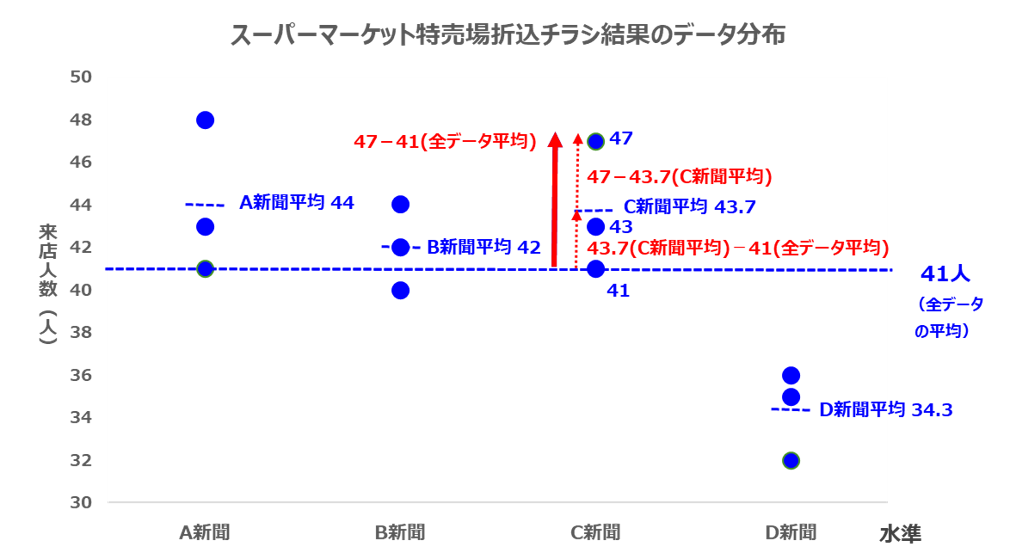
ここではC新聞の場合を見ていきましょう。(下表は再掲です)

C新聞の3回目のデータは47人で、この47人から全データの平均の41人を引いた(47-41)は(47-43.7)と(43.7-41)の和に分解できます。
(47-43.7)は、C新聞(第3水準)の第3回目のデータが、C新聞の平均からどれ位離れているのかを示しています。これを実験誤差(水準内変動)と呼びます。
もしも実験誤差がないと仮定するなら、3回調査してもC新聞平均は全て約43.7人になる、ということになります。
水準間変動とは
一方、C新聞の平均から全データの平均を引いた(43.7-41)は、C新聞の平均人数43.7人が、全体平均の41人からどれ位離れているかを示しています。これを水準間変動と言います。
すべてのデータにおいて、もし実験誤差(水準内変動)のほうが、水準間変動よりも小さければ、統計的に、どの新聞に折込チラシを入れるのかで来店人数は違ってくるということになります。
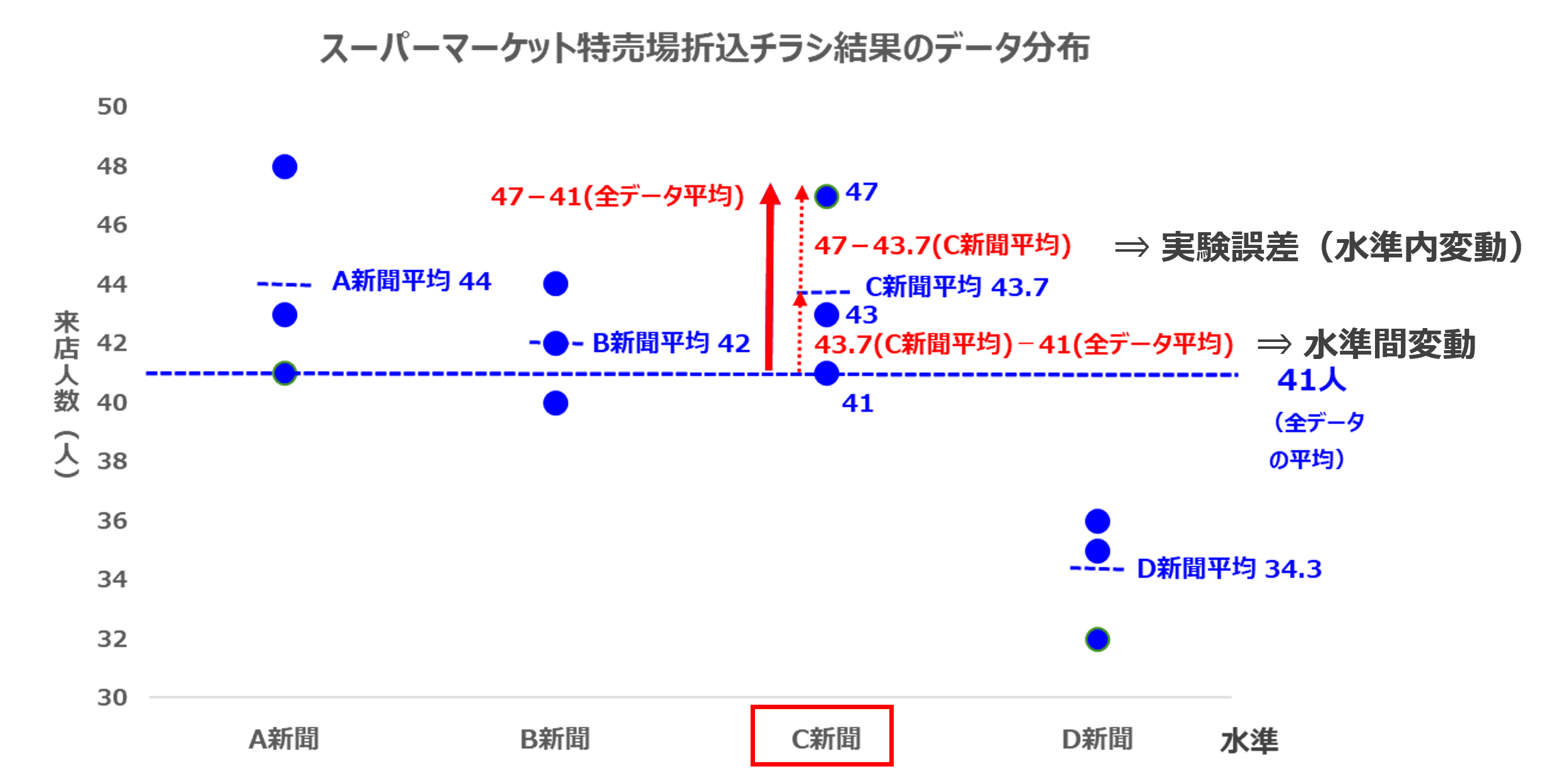
これを言い換えますと、一つ一つのデータと全データの平均(41)の差(水準間変動)のほとんどを、実験誤差(水準内変動)が説明してしまうなら、チラシの来店促進効果において、新聞間の違いはないということになります。
分散比(F値)とは
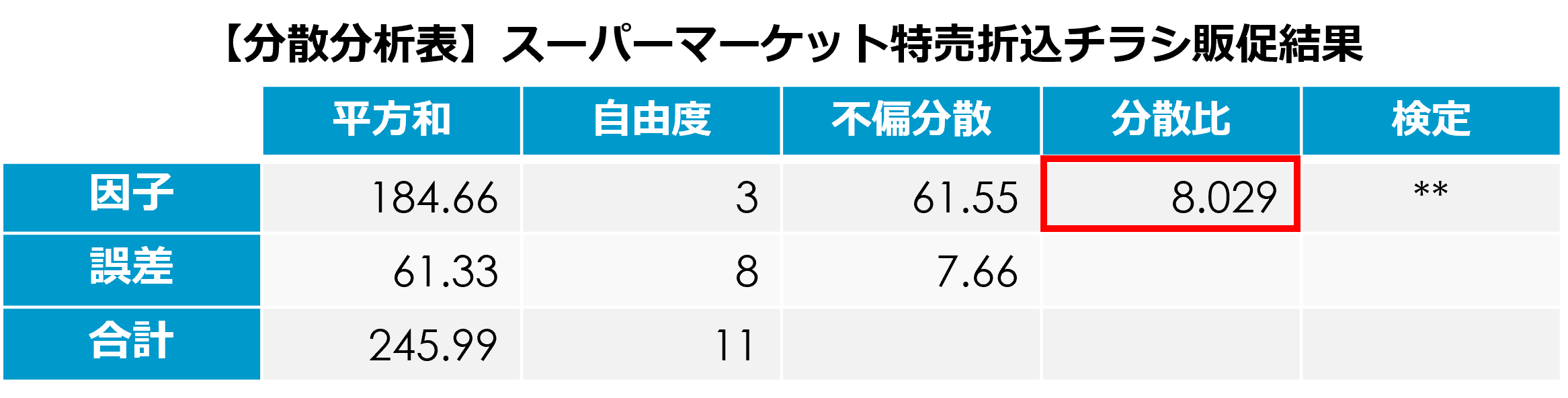
実験誤差(水準内変動)と水準間変動の比率を分散比と言います。
この分散比の値がかなり大きければ、因子(この調査の場合はAからCの新聞折込チラシ)の効果があるということになります。
このように、因子の効果を平均値の分散を用いて評価することから、この分析方法を分散分析と呼んでいます。
なお、今回の調査結果の分散分析表の分散比は、8.029です。
仮説検定としての分散分析
仮説と対立仮説とは
ところでこの調査における仮説と対立仮説は以下の通りです。

有意水準αを1%とすれば(検定統計量である)分散比8.029は、自由度(3,8)のF(α=0.01)点である7.59より大きい。
つまり仮説H0の下で滅多に起きないことが起きたことになります。
それは最初に設定した仮説が間違っていたのではないかと判断して対立仮説H1を採択する、つまり、折込チラシ販促において、A新聞、B新聞、C新聞、D新聞の母平均に差がある、との結論になるということです。
有意水準・自由度・F分布の考え方
前項で示した仮説と対立仮説を前提として、分散分析では、有意水準・自由度・F分布を用いて、分散比(F値)が統計的に有意かどうかを判断します。
このとき、有意水準αを1%と設定します。有意水準とは、「帰無仮説が正しいと仮定した場合に、どの程度まれな事象までを許容するか」を表す基準です。
分散分析では、分散比(F値)を検定統計量として用います。今回の調査結果における分散分析表の分散比は8.029 す。
この値を、自由度(3,8) 対応するF分布と比較します。自由度とは、分散分析においてデータのばらつきを評価する際の基準となる数値で、因子の水準数やデータ数から決まります。
自由度(3,8)におけるF(α=0.01)点は7.59です。
今回の分散比8.029は、この7.59よりも大きいため、帰無仮説のもとでは滅多に起こらない事象が起きたと判断できます。
その結果、最初に設定した仮説が誤っている可能性が高いと考え、対立仮説を採択します。
つまり、折込チラシ販促において、A新聞・B新聞・C新聞・D新聞の母平均には差がある、という結論になります。
\ あとから見返せる!分散分析マニュアル /
分散分析で扱うデータの前提条件
分散分析の前提(正規性・等分散性など)
分散分析で扱うデータの前提は下記です。
- 不偏性(誤差の期待値がゼロ)
- 等分散性(各水準内での誤差の大きさが等しい)
- 無相関性(誤差同士は無相関)
- 正規性(誤差は正規分布に従う)
前提条件を満たさない場合の対処法
分散分析を行う前に、データをプロットし、水準内でのデータのバラつきがほぼ等しいかどうかチェックするのがいいでしょう。
観測データの値が大きくなるに従って、データのバラつきも大きくなることがよく起きますが、このような場合、データを対数変換すれば等分散になることが多くなります。
また、データが明らかに非対称で正規分布となっていない場合は、クラスカル・ウォリス検定(一元配置の場合)や、フリードマン検定(二元配置の場合)を実行しましょう。
なお、データの分布や関係性を事前に確認したい場合には、相関分析を用いて変数同士の傾向を把握するのも有効です。
Excelを使った分散分析の手順
Excelで分析ツールを有効化する方法
分散分析は、分析ツールを使って行うことができます。分析ツールは、Excelの画面で簡単に設定することができるので、ぜひ活用しましょう。
【基本操作】
1.ファイルメニューをクリック
2.ファイルメニューで「その他」「オプション」をクリック
3.「Excelのオプション」画面の「アドイン」をクリック
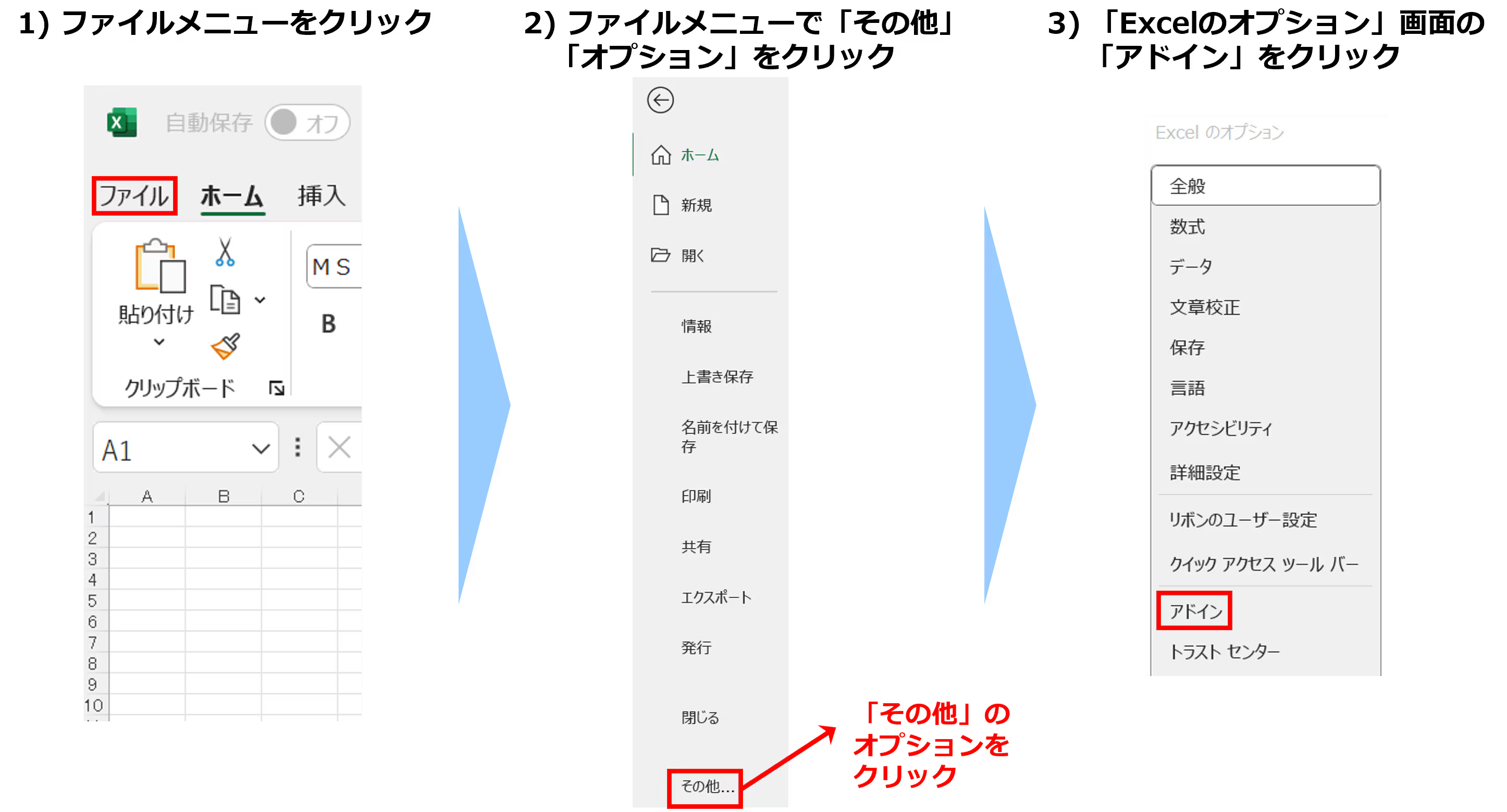
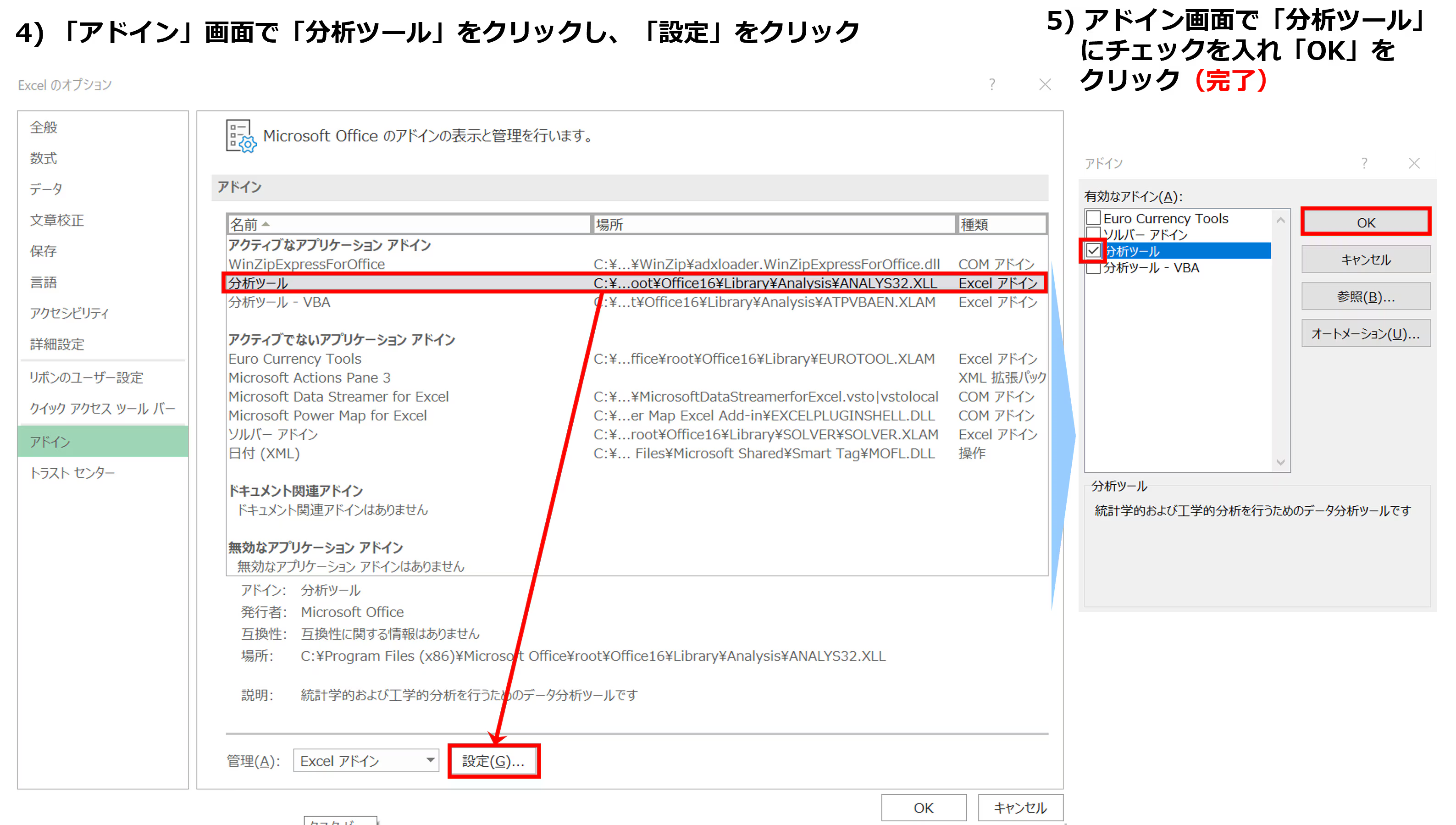
4.「アドイン」画面で「分析ツール」をクリックし、「設定」をクリック
5.アドイン画面で「分析ツール」にチェックを入れ「OK」をクリック(完了)
Excelで分散分析を実行する方法【実践編】
一元配置分散分析のやり方(Excel)
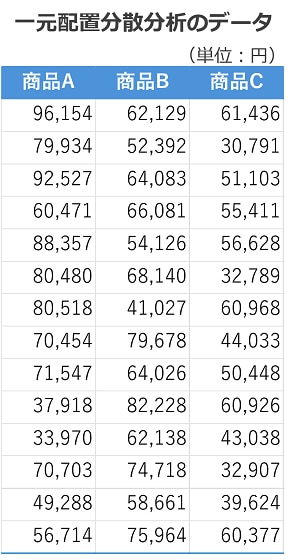
下表は、商品Aから商品Cまで3つの商品の売上金額データです。3つの商品の売上金額の平均に有意な差はあるのでしょうか。分散分析を行い検証しましょう。
因子はA、B、Cという商品の種類だけ、つまり因子は一つですので、一元配置の分散分析を行います。
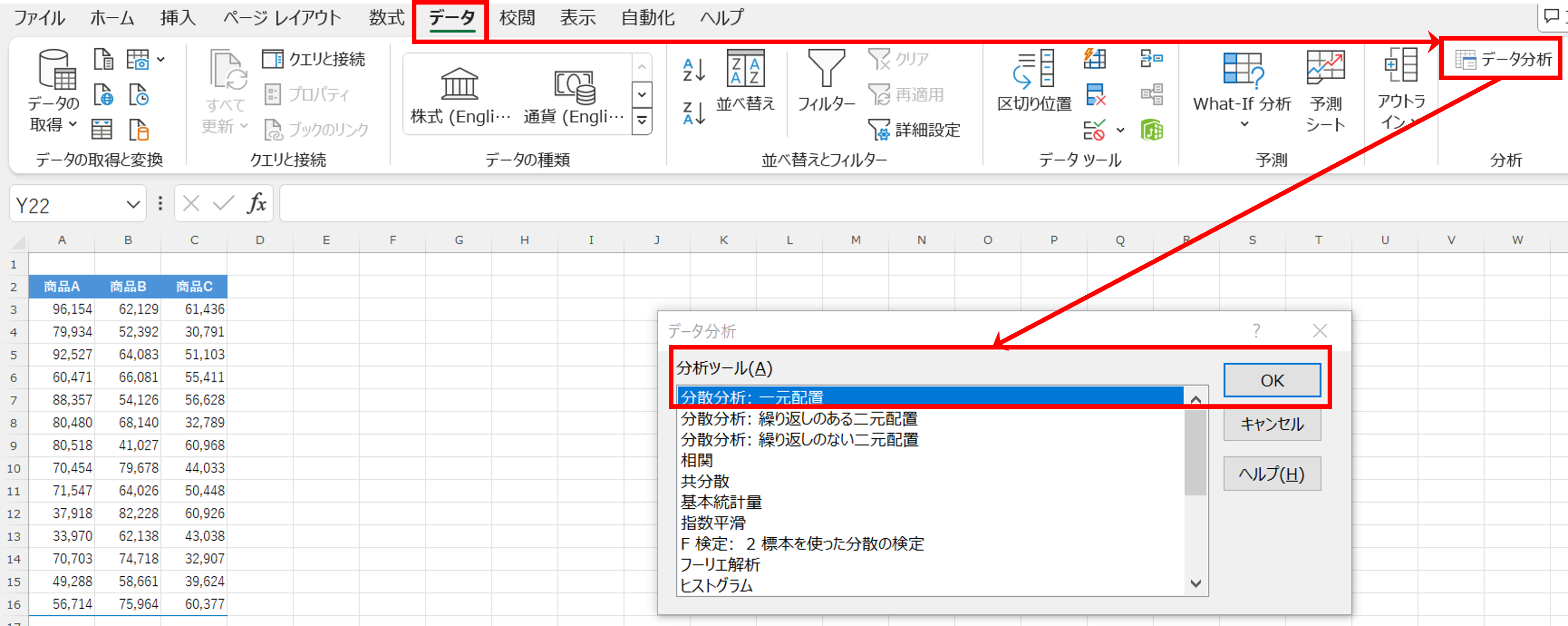
データタブの「データ分析」をクリックすると、「分析ツール(A)」のボックスが表示されます。
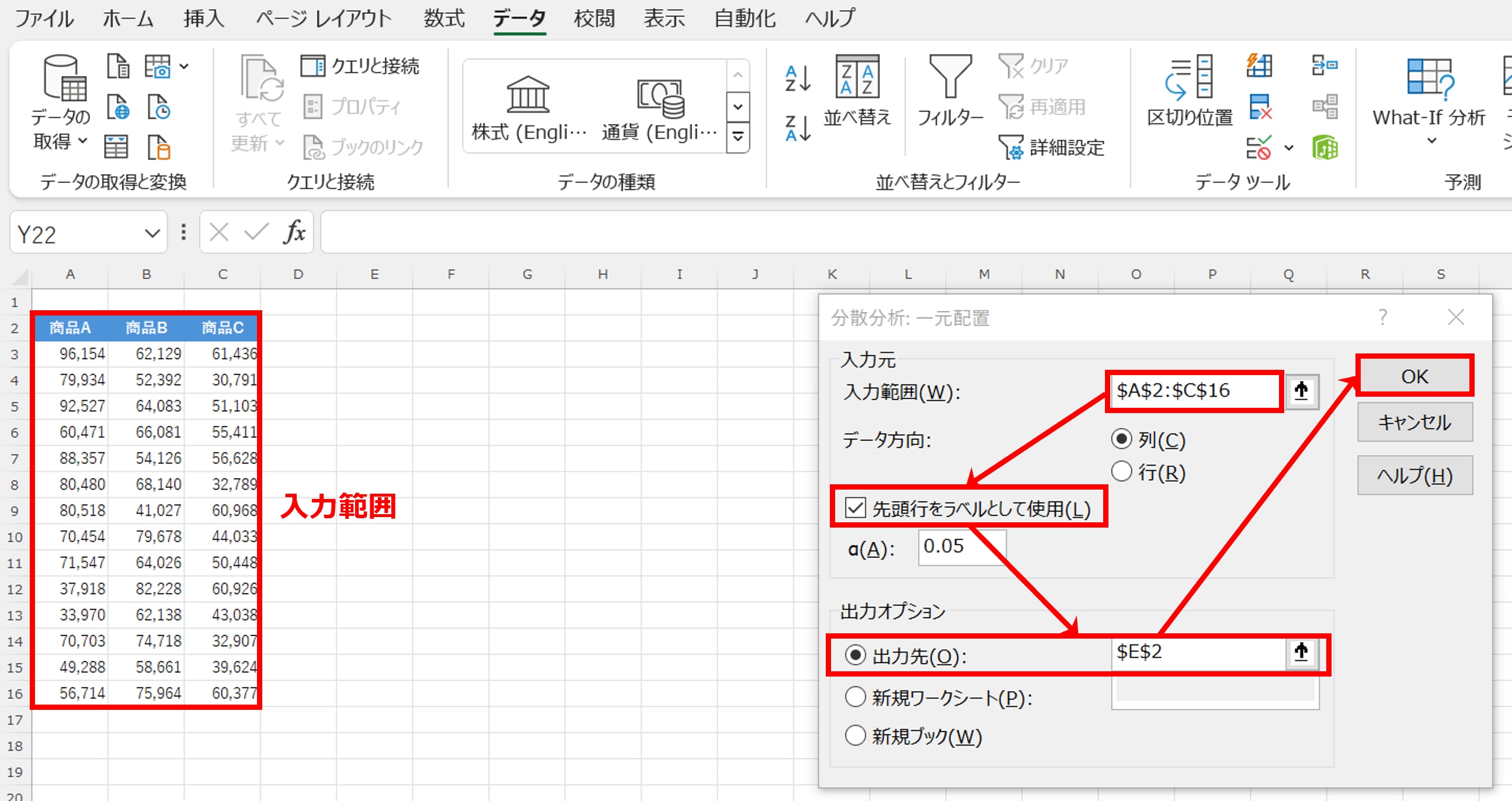
「分散分析:一元配置」を選択し、「OK」をクリックします。
「入力範囲」は表全体、「先頭行をラベルとして使用(L)」にチェックを入れます。
「出力オプション」のデフォルトは「新規ワークシート(P)」ですが、同じシート内に出力するため「出力先(O)」として任意のセルを指定します(ここではE列2行)。
「OK」をクリックします。
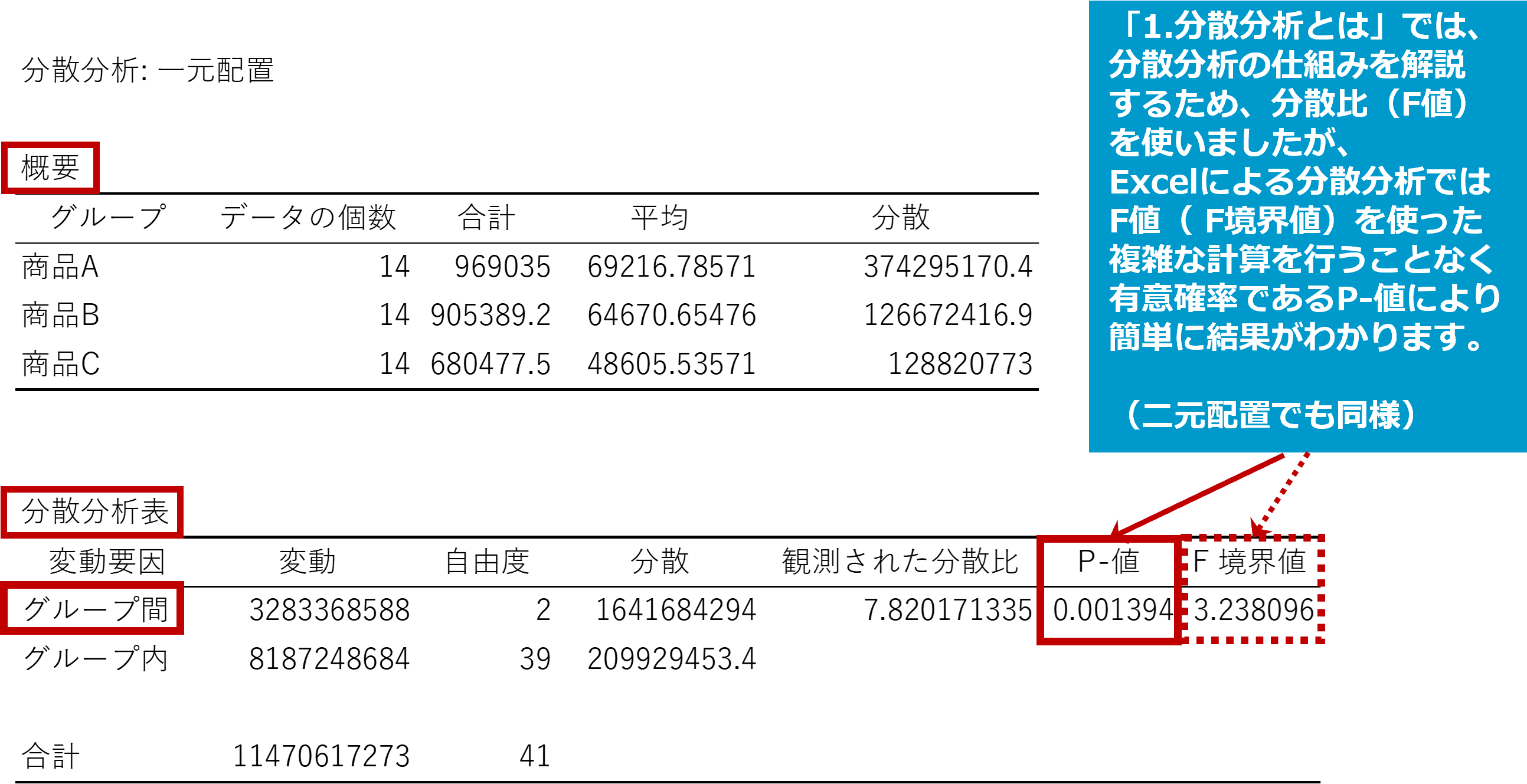
表ではP値は0.001394で0.05を下回っていますので、3つの商品(グループ間)の売上金額の平均に有意な差はあるという結果になりました。
二元配置分散分析(繰り返しあり)のやり方
次に、一元配置の分散分析例の商品Aから商品Cまで3つの商品の売上金額データに、AからCまでの3店舗という因子を加えて分析しましょう。
一元配置の分散分析結果にて、AからCまでの商品間の平均に有意な差はあることがわかりましたが、今度はAからCの3つの店舗という因子が加わります。
因子は2つなので二元配置、1店舗ごとに同じ条件のデータが4件ずつあるので、繰り返しありという分散分析となります。
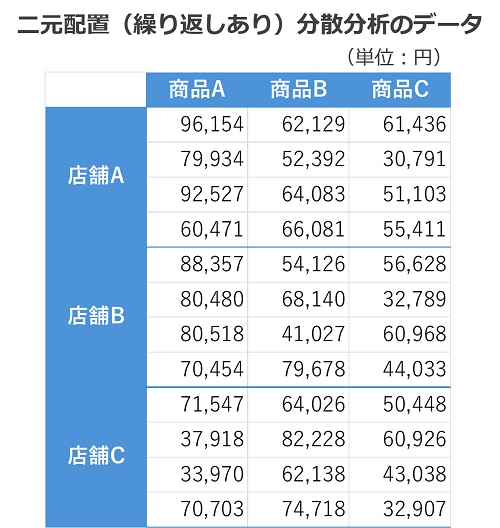
データタブの「データ分析」をクリックすると、「分析ツール(A)」のボックスが表示されます。
「分散分析:繰り返しのある二元配置」を選択し、「OK」をクリックします。
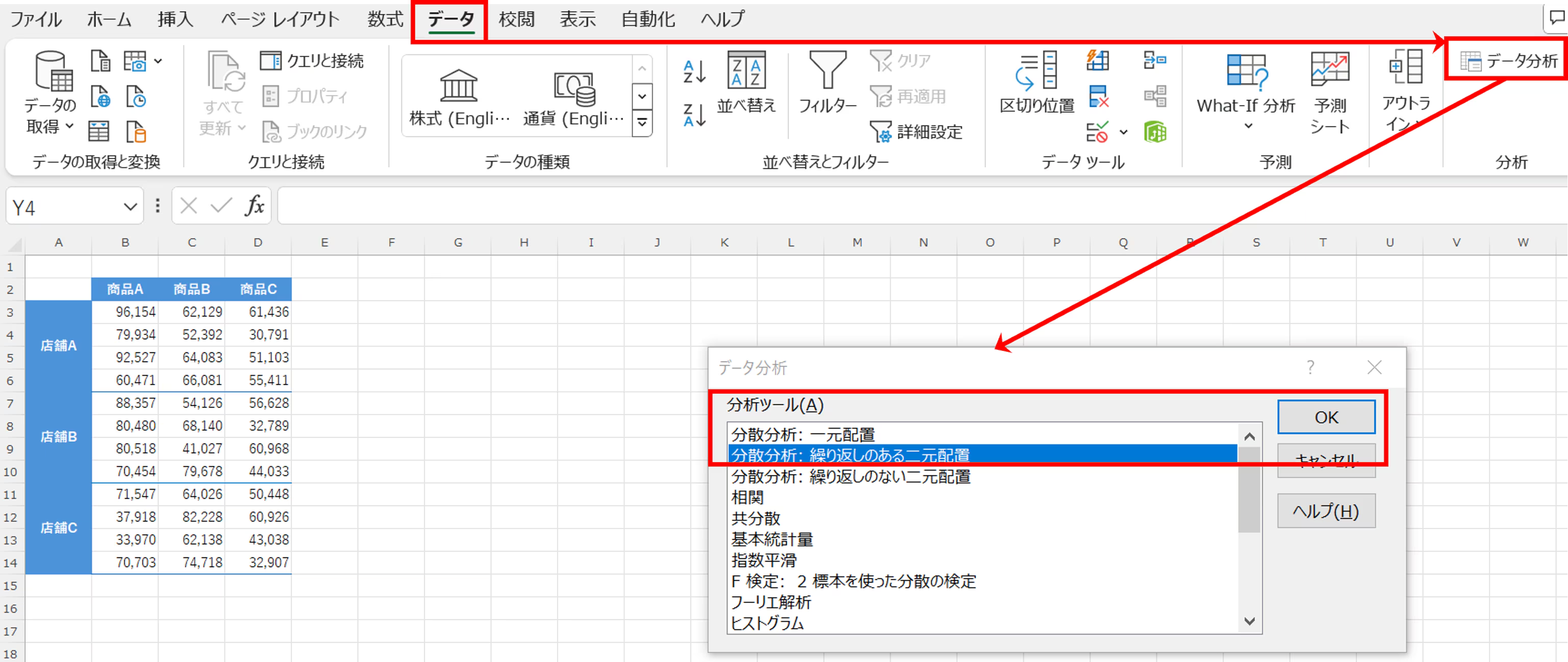
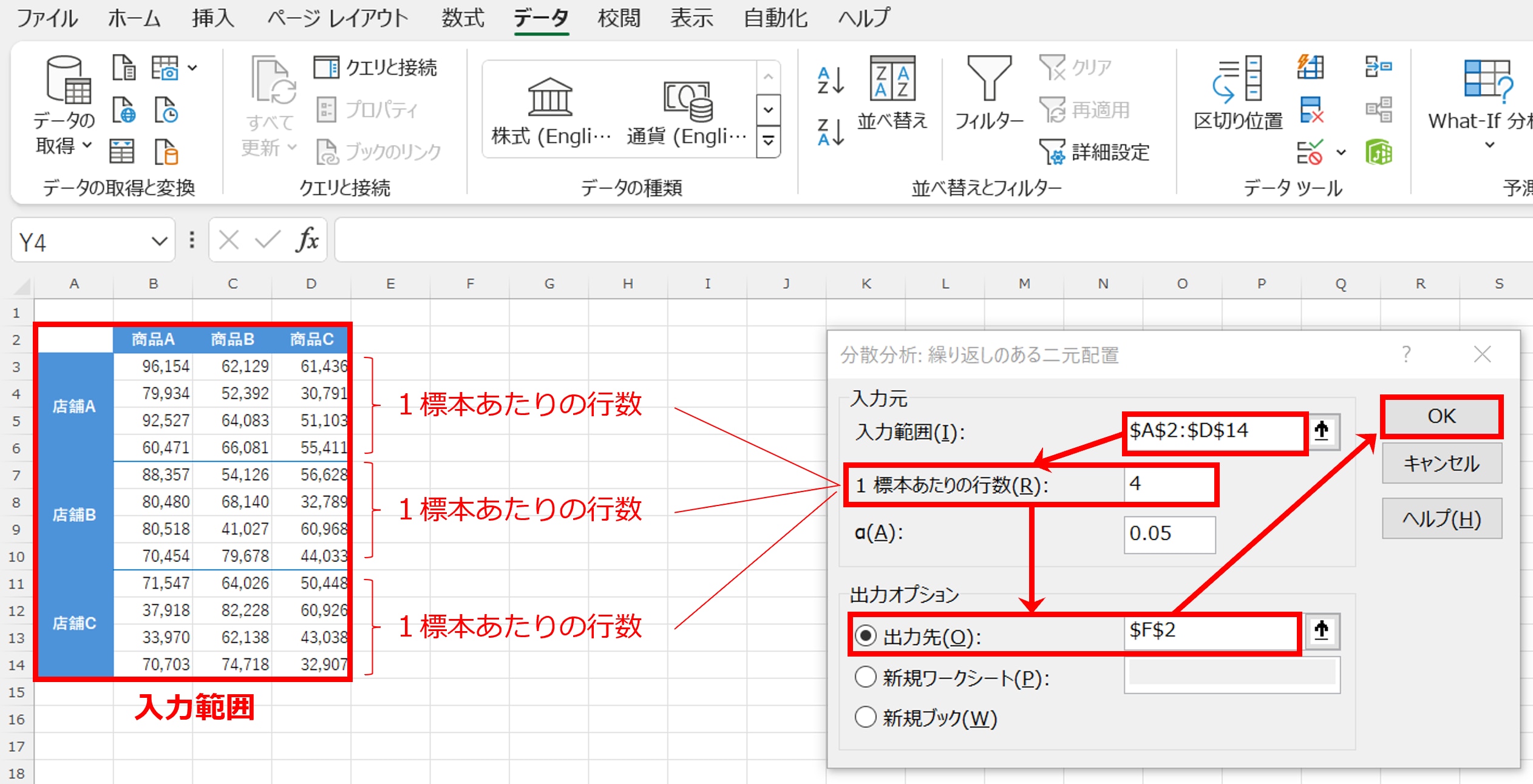
「分散分析:繰り返しのある二元配置」のボックスが表示されます。「入力範囲」は表全体です。
「1標本あたりの行数(R)」は、1店舗ごとの同じ条件のデータですので「4」を入力します。
「出力オプション」のデフォルトは「新規ワークシート(P)」ですが、同じシート内に出力するため「出力先(O)」として任意のセルを指定します(ここではF列2行)。
「OK」をクリックします。
「分散分析:繰り返しのある二元配置」の概要と分散分析表が表示されました。
表が縦に長いので概要と分散分析表を分けました。
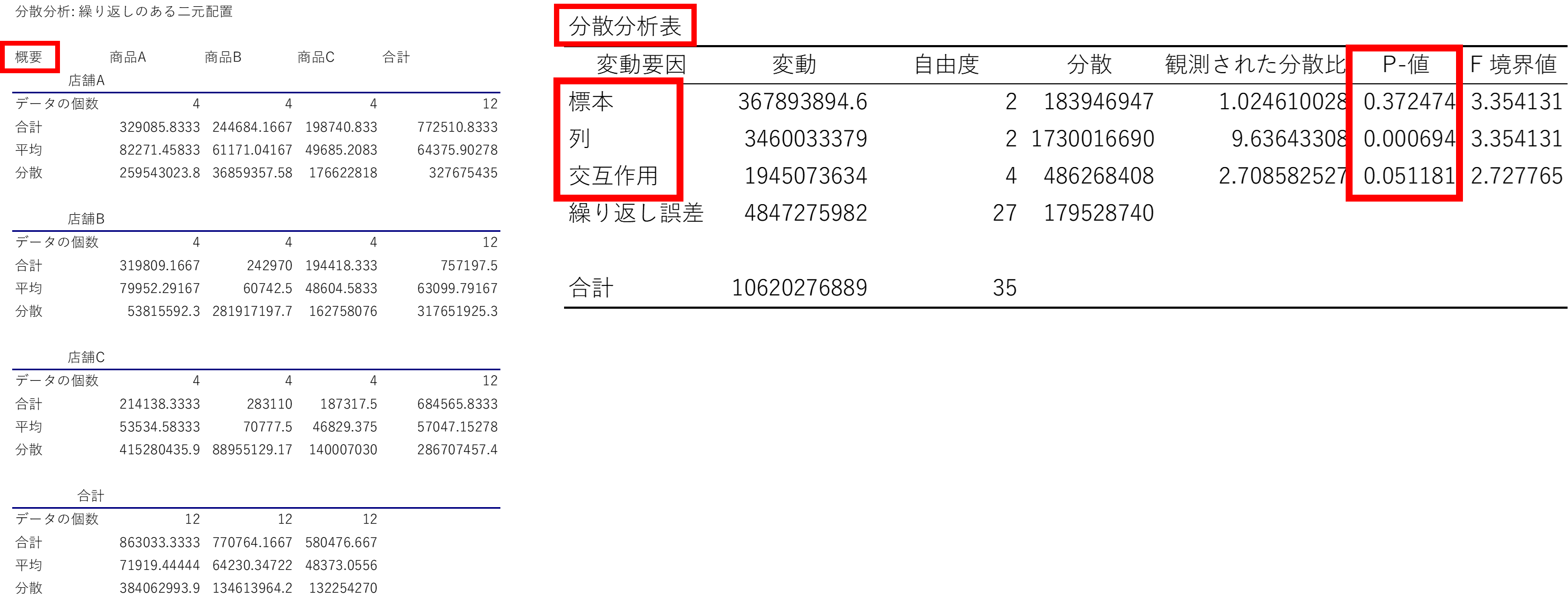
まず、分散分析表のP値に着目します。
「標本」は、3つの店舗の母平均の差です。0.372474は0.05を上回っているので、店舗間での有意な差はないことになります。
「列」は、3つの商品の母平均の差です。0.000694は0.05を下回っているので、商品間での有意な差はあることになります。
「交互作用」は、店舗と商品という二つの因子を組み合わせたときの母平均の差で、0.051181は僅かながら0.05を上回っているので、店舗と商品の組み合わせは売り上げに影響しているとは言い切れないことになります。
続いて参考までに、概要の平均をグラフ化してみましょう。表側を平均、表頭を商品AからCとして折れ線グラフを作ると、下図の右側にある二つのグラフとなります。
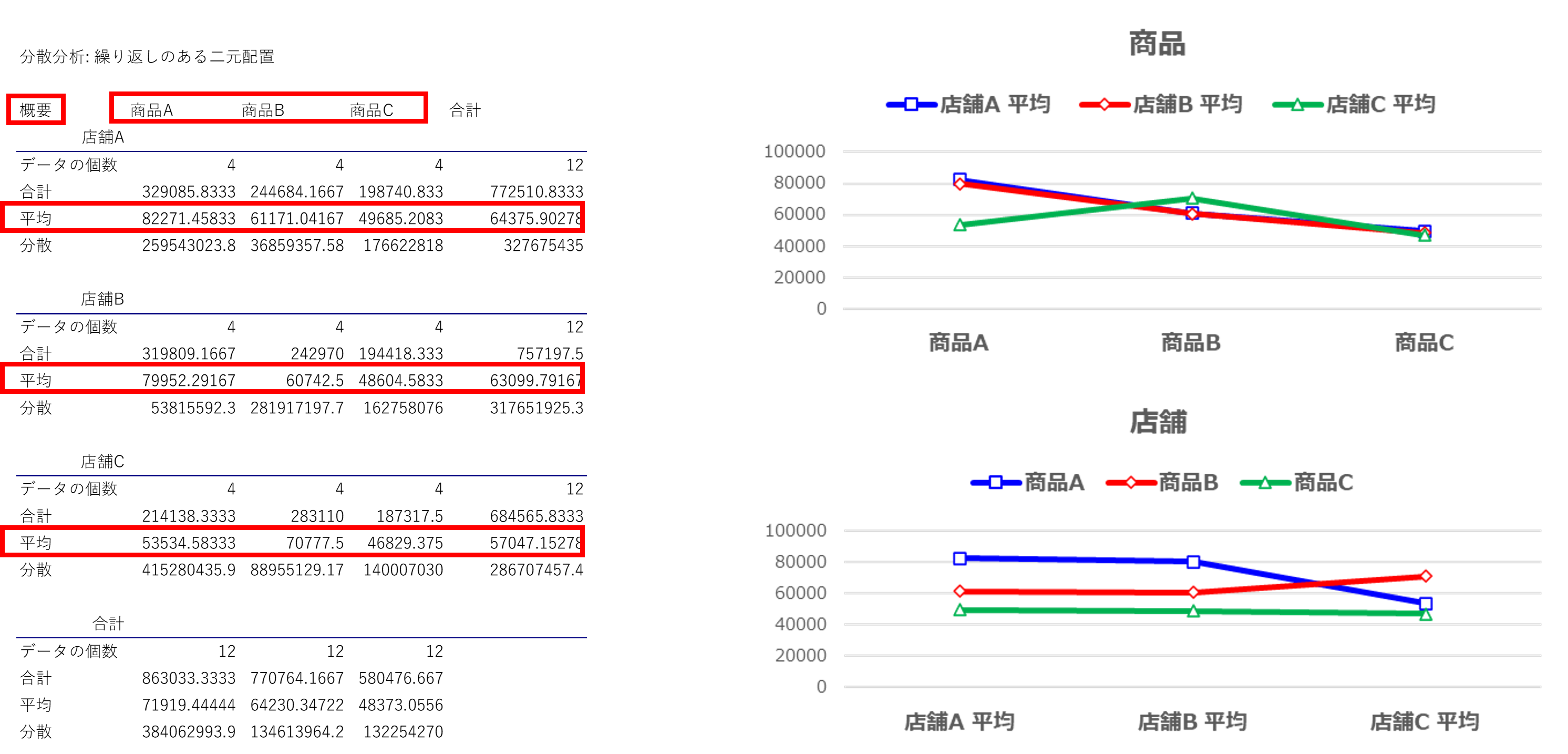
上のグラフでは、商品Aが最も売れるのは店舗Aと店舗B、商品Bは店舗C、商品Cでは3店舗ほぼ変わらないことを表しています。
下のグラフでは、店舗Aと店舗Bで最も売れるのは商品A、店舗Cでは商品Bということを表しています。
このようにグラフにすると結果が分かりやすい場合もあるので、必要に応じて活用しましょう。
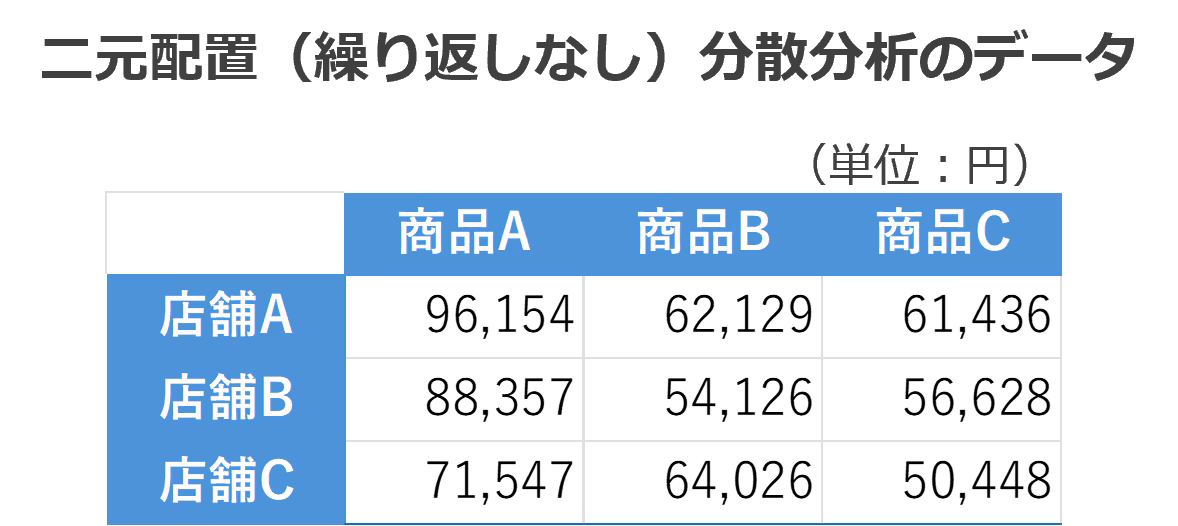
二元配置分散分析(繰り返しなし)のやり方
二元配置の【繰り返しあり】の場合、1店舗ごとに同じ条件のデータが4件ずつありましたが、1件しかない場合は、二元配置の【繰り返しなし】の分散分析を行います。
データタブの「データ分析」をクリックすると、「分析ツール(A)」のボックスが表示されます。
「分散分析:繰り返しのない二元配置」を選択し、「OK」をクリックします。
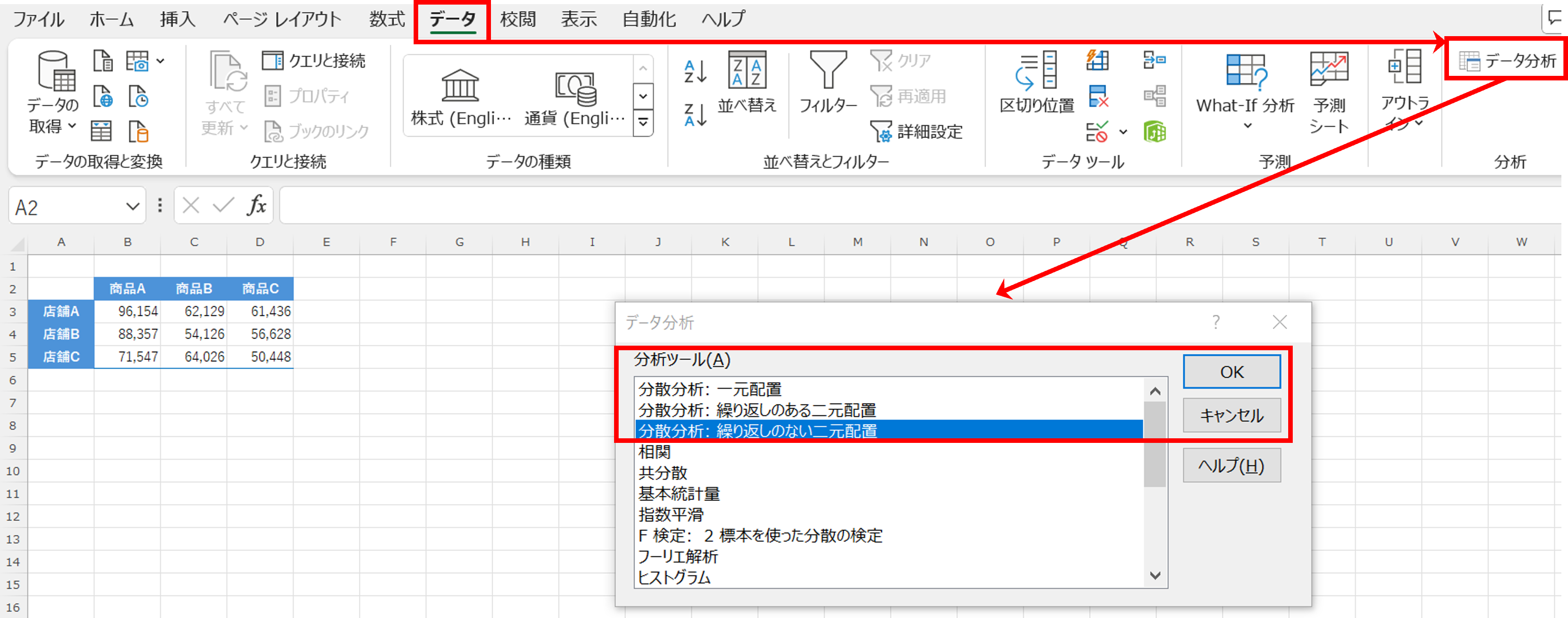
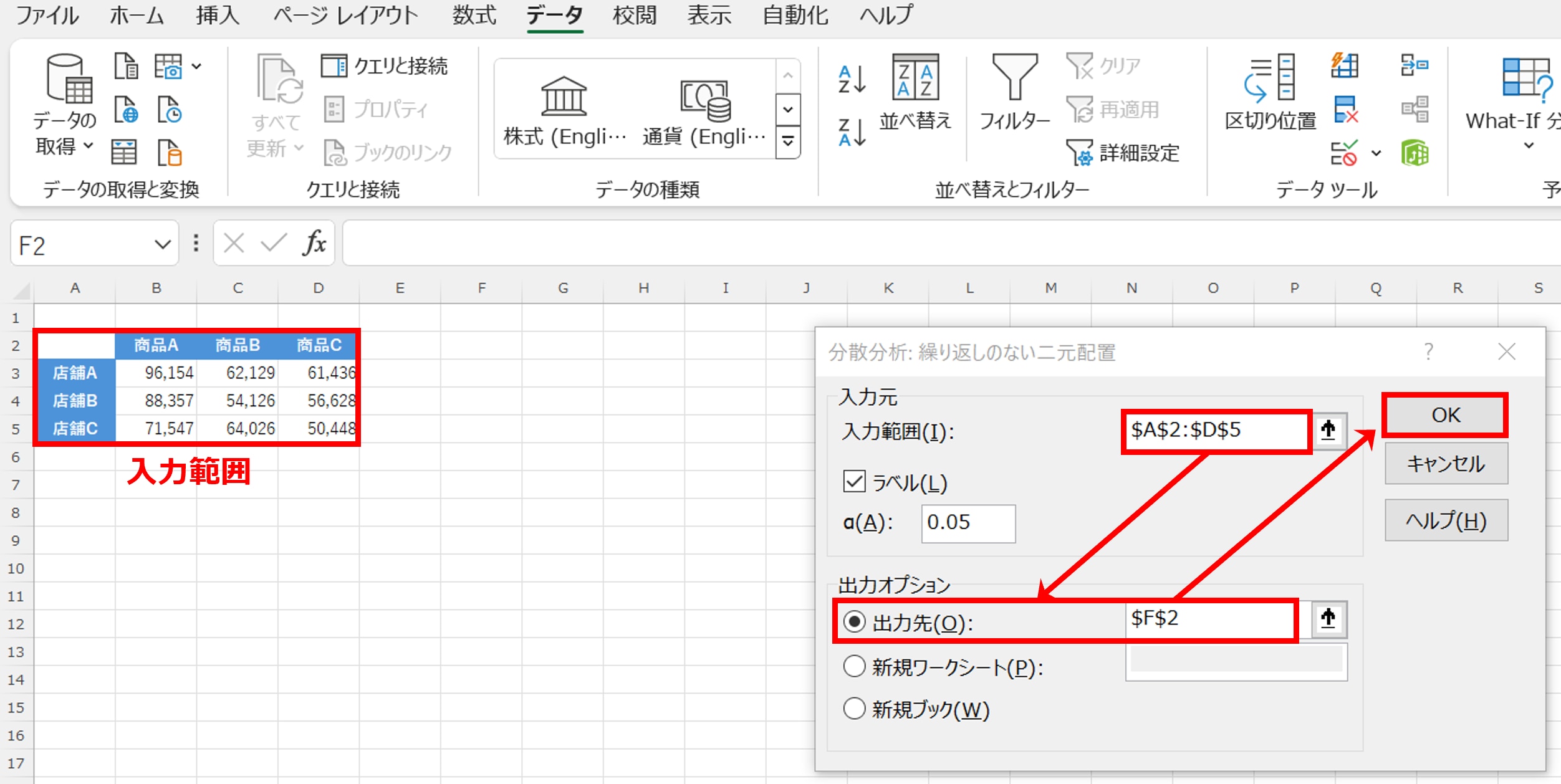
「分散分析:繰り返しのない二元配置」のボックスが表示されます。「入力範囲」は表全体。
「出力オプション」のデフォルトは「新規ワークシート(P)」ですが、同じシート内に出力するため「出力先(O)」として任意のセルを指定します(ここではF列2行)。
「OK」をクリックします。
「分散分析:繰り返しのない二元配置」の概要と分散分析表が表示されました。
ここでは分散分析表のみ使いますので、概要は省略しました。
ここでも分散分析表のP値に着目します。
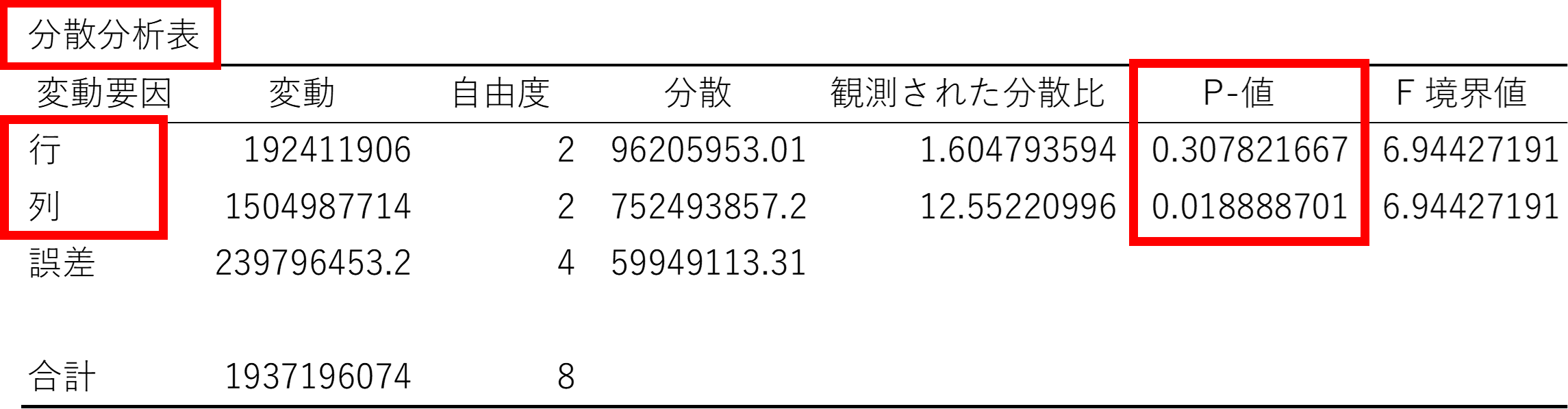
まず「行」は、3つの店舗の母平均の差で、0.307822は0.05を上回っているので店舗間での有意な差はないことになります。
「列」は、3つの商品の母平均の差で、0.018889は0.05を下回っているので商品間での有意な差はあることになります。
結論は、「交互作用」がなければ、AからCという商品の種類が売り上げに影響しており、AからCという店舗は売り上げには影響していない、ということになります。
分散分析結果の読み方と解釈
分散分析を行ったあとは、分散分析表の数値を正しく読み取り、「平均値の差が統計的に有意かどうか」「因子の組み合わせが結果に影響しているか」を判断します。ここでは、特に重要なP値(有意確率)、交互作用、グラフ化による可視化の3点について解説します。
P値(有意確率)の見方
分散分析表に表示される P値は「有意確率」と呼ばれます。
一般的に有意水準を5%(0.05)と設定し、P値が0.05以下であれば有意差があると判断します。
例えば、一元配置分散分析の結果において、分散分析表のP値が0.001394の場合、0.05を下回っているため、3つの商品(グループ間)の売上金額の平均には有意な差があるという結論になります。
このように、Excelで分散分析を行う際は、まず分散分析表のP値を確認することで、平均との差が偶然によるものかどうかを判断します。
交互作用の考え方
交互作用とは、二元配置分散分析において、2つの因子を組み合わせたときに結果へ影響が出ているかどうかを示すものです。
例えば、「店舗」と「商品」という2つの因子がある場合、
- 商品Aは店舗Aでよく売れるが、店舗Cではあまり売れない
- 商品Bは店舗Cでよく売れる
といったように、一方の因子の効果が、もう一方の因子の水準によって変わる場合に交互作用があると考えます。
分散分析表では「交互作用」の行のP値を確認し、
- P値が0.05以下:交互作用がある
- P値が0.05より大きい:交互作用があるとは言えない
と判断します。
今回の例では、交互作用のP値は0.051181であり、0.05をわずかに上回っているため、店舗と商品の組み合わせが売上に影響しているとは断定できないという結論になります。
グラフ化による結果の可視化
分散分析の結果は、数値だけで判断できますが、グラフ化することで傾向が直感的に分かる場合があります。
二元配置分散分析(繰り返しあり)の例では、概要に表示される平均値を用いて、
- 表側を平均
- 表頭を商品A~C
として折れ線グラフを作成すると、各店舗と商品の関係を視覚的に確認できます。
例えば、
- 商品Aは店舗A・Bで売上が高い
- 商品Bは店舗Cで売上が高い
- 商品Cは店舗間で大きな差がない
といった傾向が、グラフを見ることで一目で分かります。
なお、グラフ化は必須ではありませんが、分析結果を説明・共有する場面では有効な手段となるため、必要に応じて活用するとよいでしょう。
分析結果を視覚的に把握したい場合は、散布図を用いた相関分析も有効です。
分散分析に関するよくある質問(FAQ)
分散分析やExcel操作について、よくある疑問とその回答をQ&A形式でまとめました。
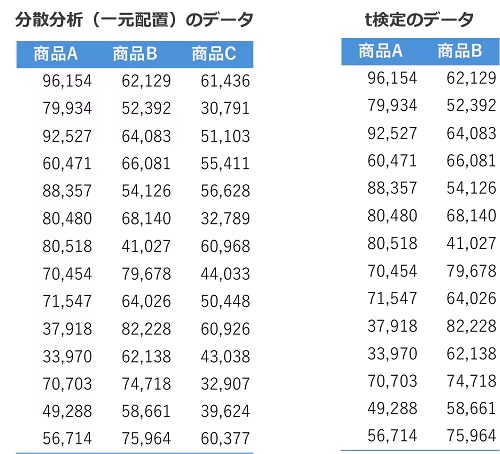
Q1.「分散分析」と「t検定」の違いは何でしょうか。
分散分析とt検定はいずれも、平均値の間に有意差があるかどうかを検定する手法です。
t検定は平均値が2つの場合に用いられ、分散分析は平均値が3つ以上ある場合に用いられます。
各手法のデータ例は下記の通りです。
Q2.SPSS・R・Pythonでも分散分析はできる?
はい、いずれのツールでも分散分析を行うことができます。
なかでも、データの形式と操作手順がExcelと近いSPSSは、実務で扱いやすいツールです。
もし分散分析で使うデータが非対称で正規分布となっていない場合には、クラスカル・ウォリス検定(一元配置の場合)を行います。SPSSでは簡単な操作でこの検定を行うことができます。
なおSPSSでは、Excelの分散分析表のP値はそのまま有意確率として表記されます。
Q3.分散分析結果のグラフ化は必須?
いいえ、グラフ化は必須ではありません。ただし、学術論文や報告資料では、分散分析結果を補足的に示すためにグラフが用いられることがよくあります。
しかし先述の事例においては、商品A~Cと店舗A~Cの売上データについて、Excel上で簡単に比較することができます。よって「店舗Aでの商品A」の売上合計が最も高いことは、すぐに分かります。
提示した折れ線グラフは、売上データの平均値を示したものです。そのため、分析結果を説明・共有する必要がある場合にのみ、グラフを作成すれば十分です。
Q4.分散分析は、どのような領域でよく使われますか。
分散分析は平均値間の有意差を検定する手法のため、特定の領域・業界に限定されるものではありません。
ただし、学術研究や商品開発の研究所など、統計的な正確性が求められる領域、例えばメディカルや医薬品業界、製造業の品質管理などで使われる傾向が多いです。
無料ダウンロード資料のご案内
本記事の内容をまとめた「分散分析マニュアル(Excel対応)」を無料でダウンロードできます。
まとめ|分散分析(ANOVA)のポイント整理
分散分析(ANOVA:Analysis of Variance)とは、平均値が3つ以上ある場合に、それぞれの平均値の間に有意な差があるのか、また差があるとすれば、どの平均値とどの平均値の間の差があるのかを判定する手法です。
平均値が2つまでの場合の分析はt検)が用いられます。
分散分析の基本的な考え方は、一つの因子による水準内変動のほうが、別の因子を含めた全データの水準間変動よりも小さければ(分散比が大きくなる)、統計的な有意差があることになる、ということです。
分散分析には主に3つの種類があります。
因子が1つの場合の「一元配置分散分析」、因子が2つで各因子の組み合わせごとに複数のデータ(繰り返し)がある場合の「二元配置分散分析(繰り返しあり)」、そして因子が2つでも1つのデータしかない(繰り返しがない)場合の「二元配置分散分析(繰り返しなし)」です。
分散分析で最も重要な判断基準となるのが、Excelの分散分析表のP値(有意確率)です。
一般的に、有意水準を5%と設定した場合、P値が0.05以下であれば有意差があると判断します。
なお、SPSSではP値ではなく「有意確率」としてそのまま表記されます。
分散分析が使われる領域は、平均値間の有意差の検定という性質もあり、特定の領域・業界に限定されるものではありませんが、学術研究や商品開発の研究所など、統計的な正確性が求められる領域でよく用いられます。
例えばメディカルや医薬品業界、製造業の品質管理などが代表的な活用分野です。
【参考文献・ウェブサイト】
『1からのマーケティング分析 第2版』(恩藏直人・冨田健司 編著、碩学舎、2022年3月)






