判別分析とは？基本、エクセル関数、結果の見方を解説！

はじめに

判別分析について、基礎知識やExcel関数、実施手順を、例題を交えながら分かりやすく解説していきます。

この記事を読んで分かること、できるようになること

●判別分析の基礎を正しく理解することができる。
●判別分析の各算出方法、エクセルでのやり方を習得できる。
●判別分析のマニュアル（資料）を無料でダウンロードできる。

＼今すぐ資料を見たい／

判別分析とは

判別分析（discriminant analysis）とは、人やモノ、現象などがどのグループ（群）に属するのかを判別する統計手法のことです。

判別分析の主な種類

判別分析には、線形判別関係式による判別とマハラノビス汎距離による判別があります。

線形判別とは、データが直線のどちら側にあるかを見ることで、どちらのクラスに属するか判別することです。

マハラノビス汎距離による判別とは、データの外れ具合やばらつき具合、相関関係を反映して算出、判別する方法です。マハラノビスは、統計学で用いられる距離の1種で、インドの統計学者プラサンタ・チャンドラ・マハラノビスの名前からきています。

線形判別関係式による判別分析

ここでは例として「煙草を1日何本吸っていて、お酒を1か月間で何日飲んでいれば、不整脈症状のあるグループに分類されるのか、症状のないグループに分類されるのか」を判別していきます。

不整脈症状の有無が目的変数、喫煙本数と飲酒日数が説明変数です。
ロジスティック回帰分析と同様、目的変数はカテゴリーデータ、説明変数は数値データです。

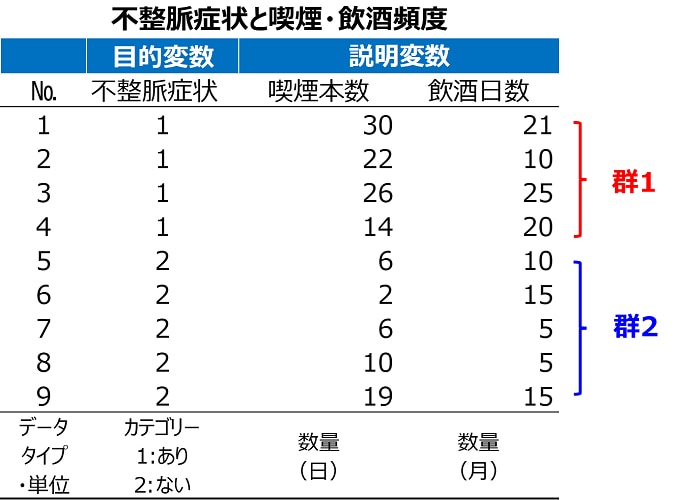
判別分析の中で最もポピュラーな線形判別関係式による判別分析を行っていきましょう。

縦軸（x1）に喫煙本数、横軸（x2）に飲酒日数をプロットした散布図を作成します。
赤い点は群1（不整脈症状あり）、青い点は群2（不整脈症状なし）の人達です。

これら2群を分けるのに最も適した点線が、線形判別関係式です。
No.9の対象者のみ例外となりましたが、線形判別関係式の上下で群1と群2に分かれました（算出方法は後述の「Excelを使った判別分析」で詳しく解説します）。

マハラノビス汎距離による判別分析

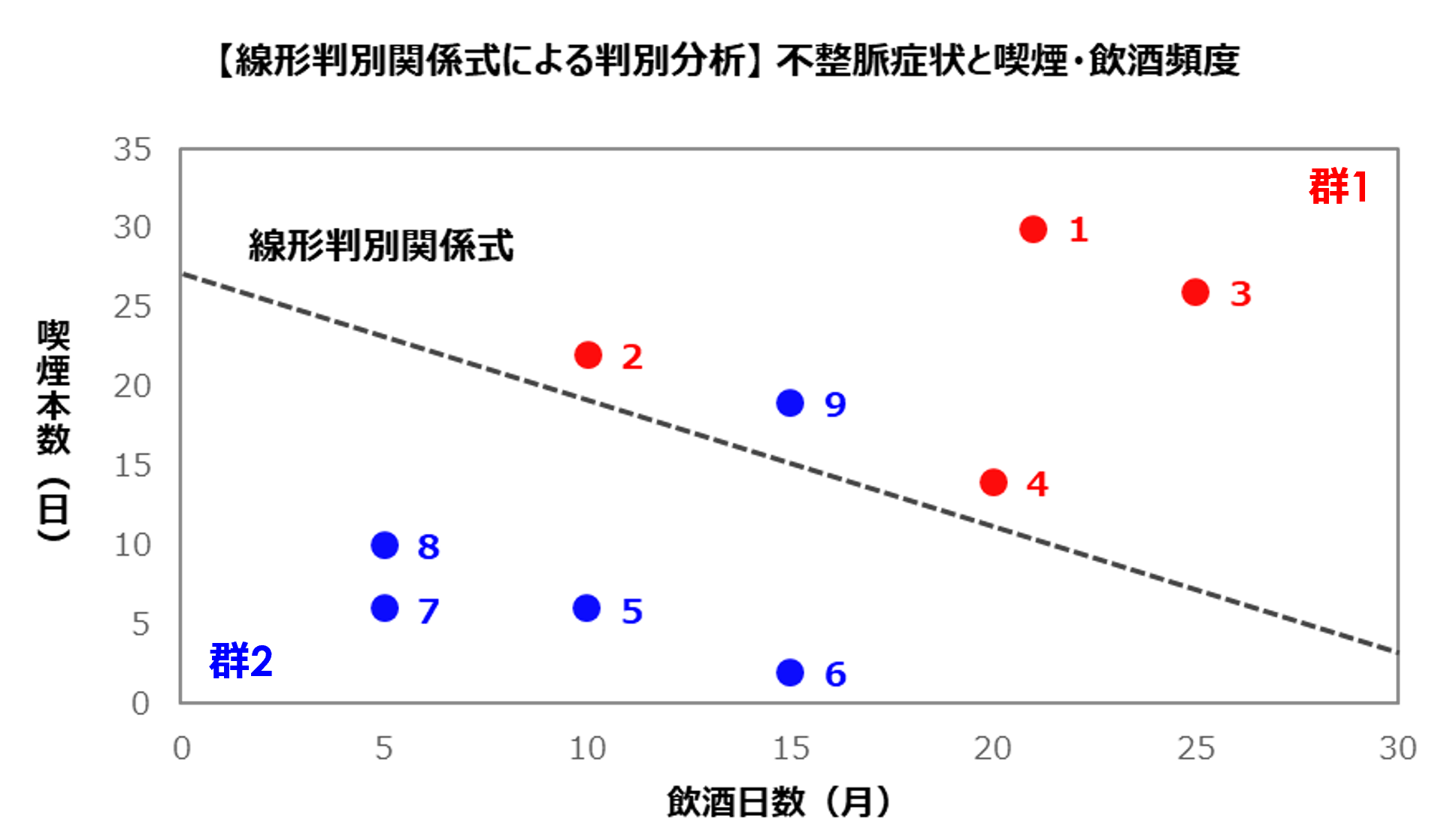
次に、マハラノビス汎距離による判別分析を行いましょう。

まず、群1と群2の平均値を算出します。群1の平均値は喫煙本数23本、飲酒日数19日、群2の平均値は喫煙本数8.6本、飲酒日数10日となりました。

前述の散布図に群1と群2の平均値をプロットしました。これら平均値が重心となります。

やはりNo.9の対象者のみ例外となりますが、各データが群1と群2それぞれの重心のどちらの距離が近いかによって判別することになります（算出方法は後述の「Excelを使った判別分析」で詳しく解説します）。

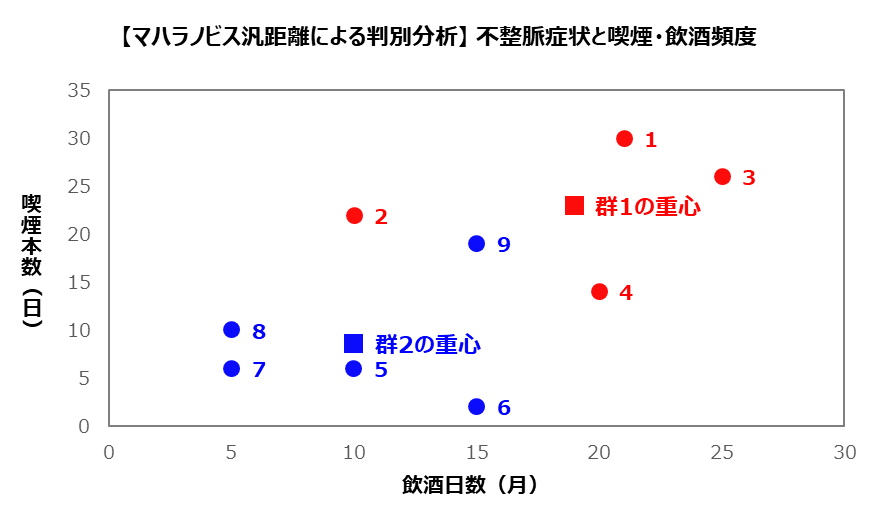
線形判別関係式とマハラノビス汎距離のアウトプット比較（参考）

参考までに、線形判別関係式による判別分析と、マハラノビス汎距離による判別分析のアウトプットをマージしてみました。No.9の対象者以外、群1と群2のデータが明確に分類されています。

＼今すぐ資料を見たい／

Excelを使った判別分析のやり方

「線形判別関係式」をExcelで実施する手順

まずはじめに、線形判別関係式による判別分析をエクセルで実施するやり方を説明します。

1.前提

分析に必要な判別係数を算出するために、まず、x1を喫煙本数、x2を飲酒日数とします。

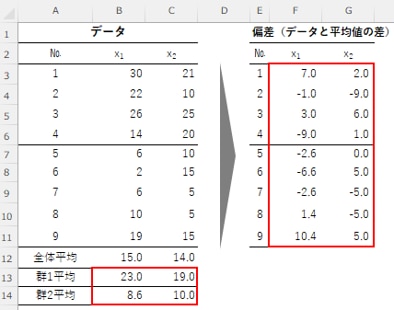
2.群ごとの偏差の算出

群ごとの偏差を算出します。偏差はデータと平均値の差です。
F列3行には「=B3-$B$13」、G列3行には「=C3-$C$13」、F列7行には「=B7-$B$14」、G列7行には「=C7-$C$14」という数式を入力します。

3.分散と共分散の算出

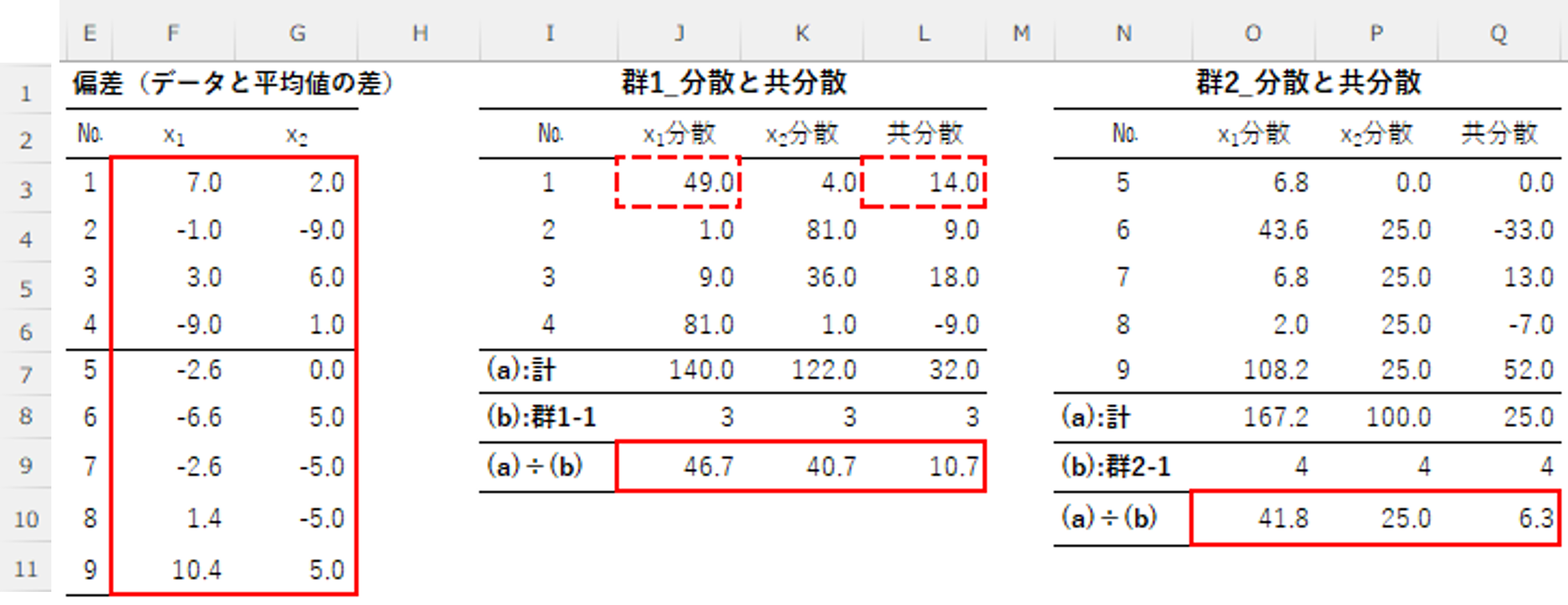
群1と群2の分散と共分散を算出します。

分散は、偏差平方（偏差の2乗）の合計(a)を、データ数から1を引いた数字(b)で割って算出します。

共分散は、x1とx2の偏差（データと平均値の差）を掛け合わせた数値の合計(a)を、データ数から1を引いた数字(b)で割って算出します。

＊群1_分散と共分散のNo.1の「x1分散」「49.0」の数式は「=POWER(F3,2)」。
＊群1_分散と共分散のNo.1の「共分散」「14.0」の数式は「=F3*G3」。

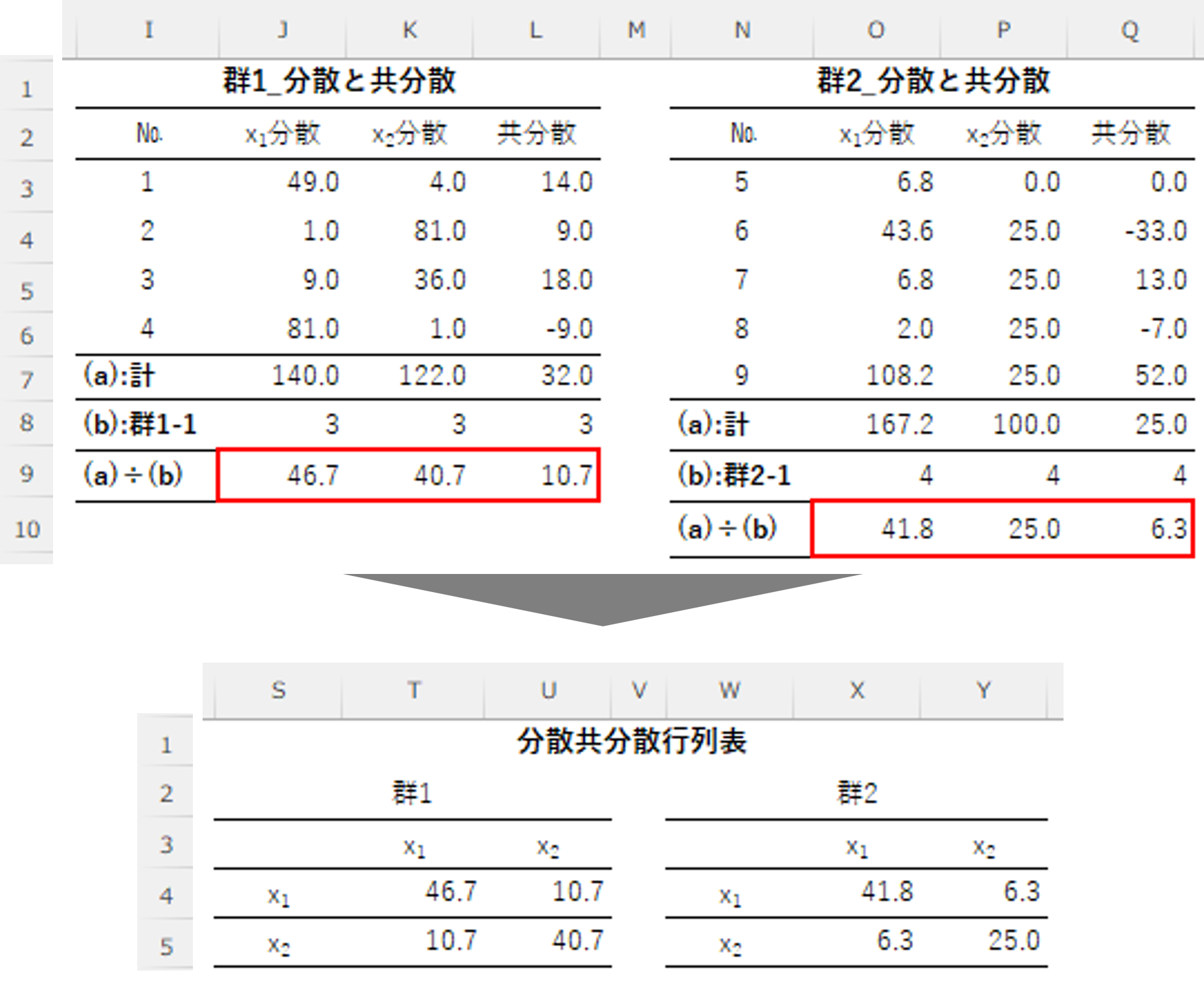
4.分散共分散行列表の作成

群1と群2の分散と共分散から、分散共分散行列表を作成します。

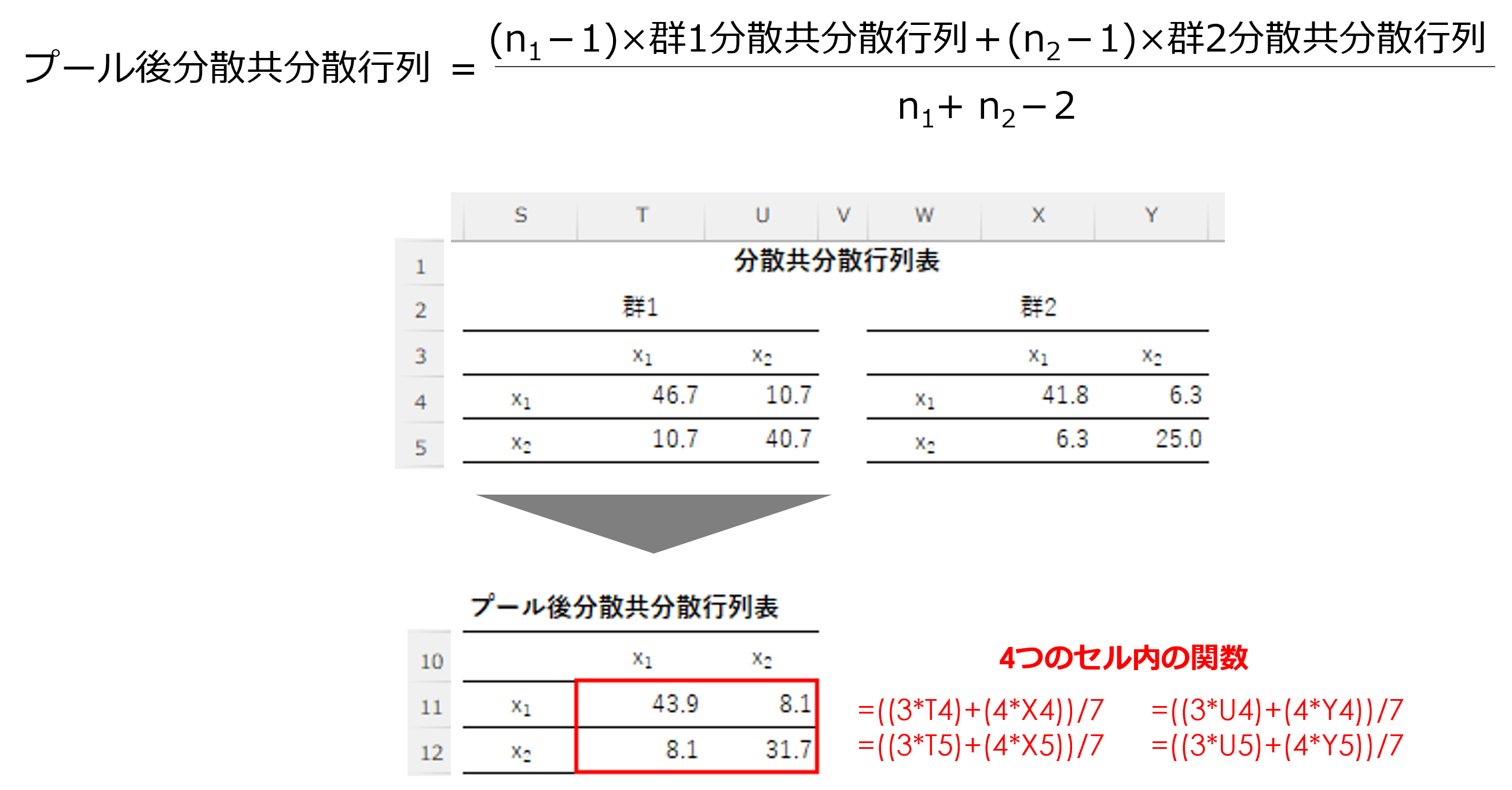
5.プール後分散共分散行列表の作成

分散共分散行列表からプール後分散共分散行列表を作成します。
群1の個体数をn1、群2の個体数をn2として、以下の計算式でプール後分散共分散行列を算出します。

6.逆行列の算出

次に逆行列を算出します。逆行列はExcel関数の「=MINVERSE」を使います。

7.判別係数の算出

判別係数は、逆行列と2群間の平均値の差分との積により算出されます。
判別係数の算出では、Excel関数の「=MMULT」を使います。

8.定数項の算出

最後に定数項を、以下の算出式を使って算出します。

定数項＝-0.5×{x1の判別関数×(群1x1の平均+群2x1の平均)}+{x2の判別関数×(群1x2の平均+群2x2の平均)}

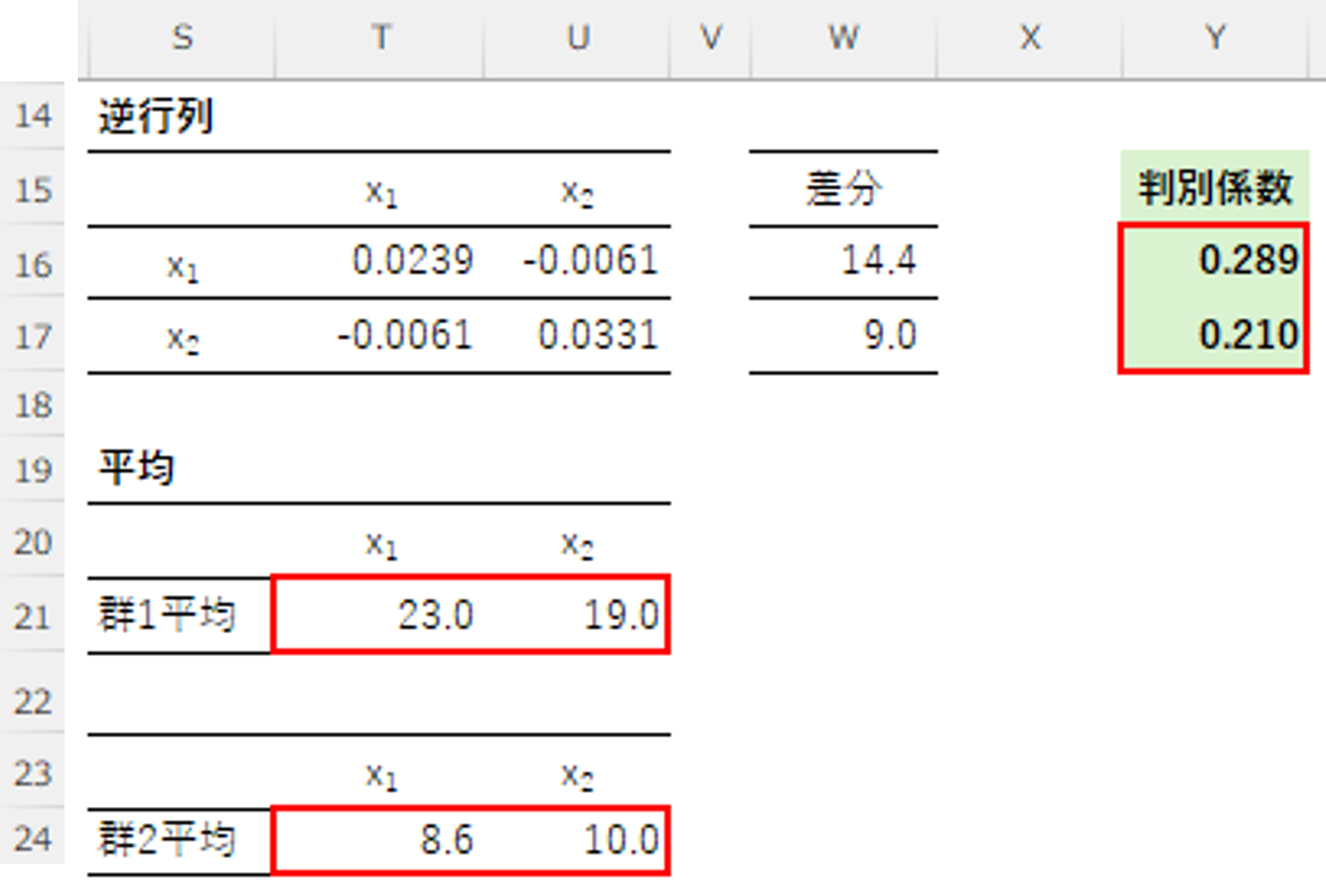
「=-0.5*(Y16*(T21+T24)+(Y17*(U21+U24)))」の計算式で算出された定数項は、「-7.6」でした。

9.線形判別関係式（結果）

線形判別関係式が求められました。

不整脈症状=0.289×喫煙本数+0.210×飲酒日数－7.6

「マハラノビス汎距離」をExcelで実施する手順

続いて、マハラノビス汎距離の算出をエクセルでおこなう手順を説明します。

1.前提

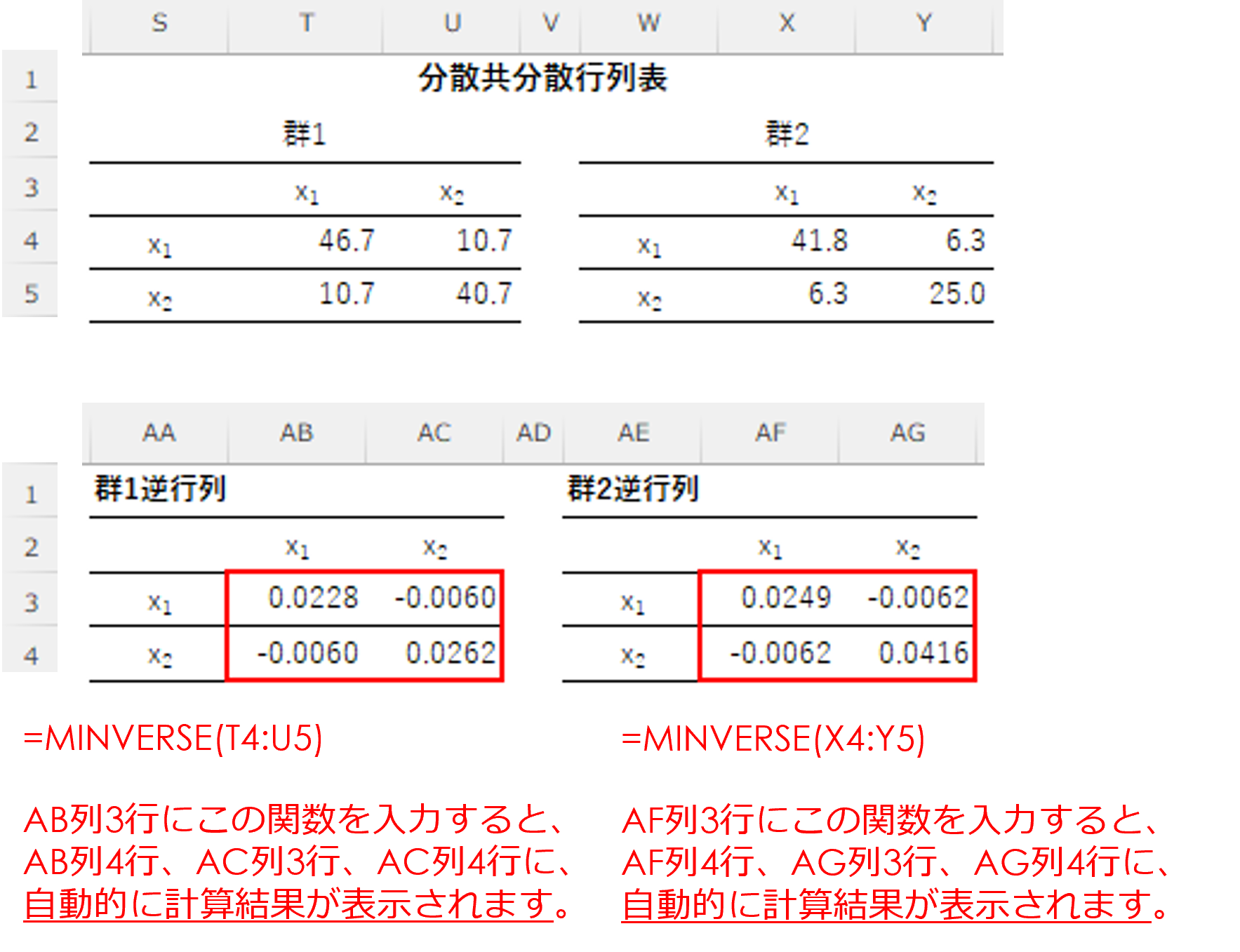
前述の「4.分散共分散行列表の作成」の群1と群2の「分散共分散行列」から、逆行列を算出します。
逆行列の算出では、Excel関数の「=MINVERSE」を使います。

2.調査対象者No.1のデータと群1平均との距離を算出する

ここでは、調査対象者No.1のデータが、群1と群2のどちらの重心との距離（マハラノビス汎距離）が近いのかを判別します。

まず、群1平均との距離を算出します。「群1平均との差分」と「群1逆行列」の数値を掛け合わせます。
ここで使うExcel関数は、逆行列の「=MMULT」、行と列を入れ替える「TRANSPOSE関数」です。

調査対象者No.1のデータと群1重心までのマハラノビス汎距離は、1.053となりました。

3.調査対象者No.1のデータと群2平均との距離を算出する

次に、調査対象者No.1のデータと群2平均との距離を算出しましょう。「群2平均との差分」と「群2逆行列」の数値を掛け合わせます。

ここで使うExcel関数は、逆行列の「=MMULT」、行と列を入れ替える「TRANSPOSE関数」です。
算出方法は、前述の群1平均と同様です。

調査対象者No.1のデータと群2重心までのマハラノビス汎距離は、13.484となりました。

4.No.2からNo.9のデータと、群1、群2平均との距離を算出する

同じように、調査対象者No.2からNo.9のデータと、群1、群2平均との距離を算出してみました。

さらに、各調査対象者が群1と群2に判別される確率も算出しました。確率の算出では、指数関数を計算するEXP関数を使います。

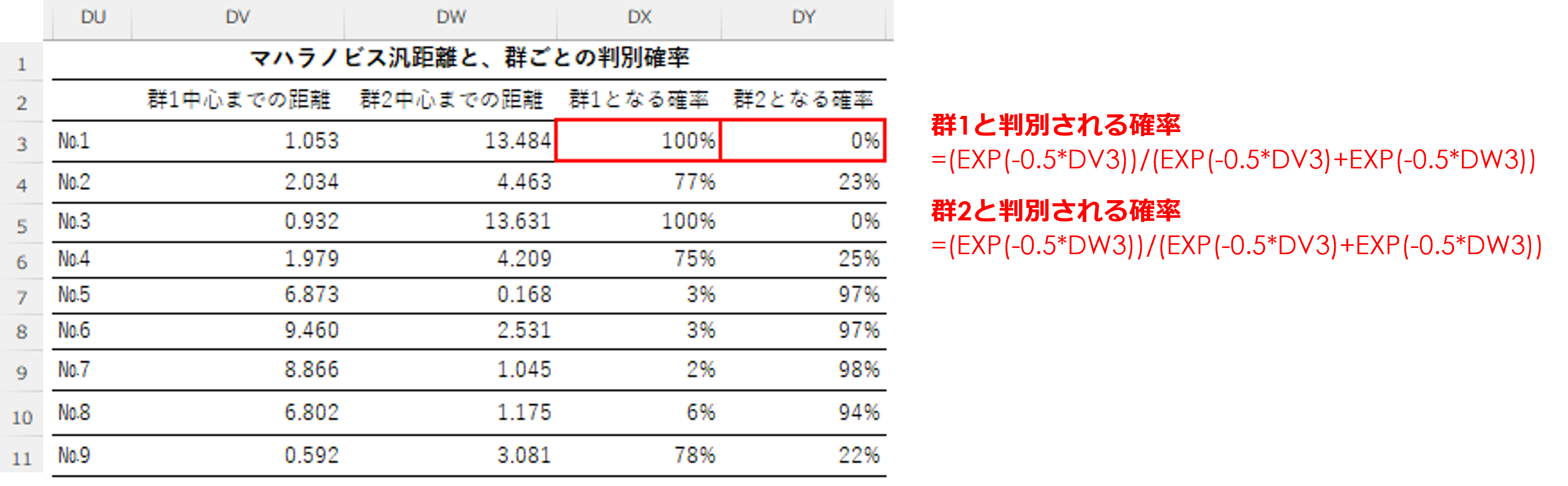
5.マハラノビス汎距離（結果）

調査対象者No.1では、群1までの距離が群2までの距離より短いので、群1に判別される可能性が高いことがわかります。

＼今すぐ資料を見たい／

判別分析にまつわる、よくある質問

Q：判別分析のデメリットを教えて下さい。

判別分析の説明変数は、重回帰分析やロジスティック回帰と同様、基本的に数値データです。
但しカテゴリーデータであっても、性別のように男性は「1」、女性は「0」と数値化すれば説明変数として使えます。

しかし、カテゴリーデータの数値データへの変換は、性別の「1」「0」のように2値の場合のみということがデメリットでもあります。
例えば血液型のように4カテゴリーでは、判別分析においては説明変数として使えません。

Q：判別分析は、Excel以外のソフトで行うことはできますか。

はい、もちろんできます。

まずExcelですが、Excel統計（有料）を使えば、複雑な関数と計算式を使うことなく、わかりやすいウィンドウでの操作により判別分析を行えます。
もちろん、SPSSやRでも行えます。SPSSは判別分析に限らず、多変量解析においてスタンダードのソフトであり、近年、Rもスタンダード化しています。

Q：判別分析の活用例を教えて下さい。

判別分析の目的は、ロジスティック回帰分析と同様、「対象者などのデータの分類」ですので、実務と研究の分野、特に医療（疾病）や医薬品の分野で、長年利用されてきました。

マーケティング分野では、顧客のカテゴリー分類で最も効果を発揮している多変量解析の一つです。見込み顧客の分類、現在の顧客の分類で大きな威力を発揮しています。

また、金融機関における与信で重宝されていることは、注目に値します。

無料ダウンロード『判別分析マニュアル』

本記事で解説した内容をまとめた資料「判別分析マニュアル～基礎、Excel関数、手順～」は、下記よりダウンロードすることができます（無料）。

おわりに（まとめ）

判別分析（discriminant analysis）とは、人やモノ、現象などがどのグループ（群）に属するのかを判別する統計手法のことです。

判別分析は、ロジスティック回帰分析と同様、目的変数はカテゴリーデータ、説明変数は数値データです。判別分析には、線形判別関係式による判別とマハラノビス汎距離による判別があります。

線形判別関係式による判別は、判別分析の中で最もポピュラーな手法です。Excelでは、偏差・分散・共分散の算出、分散共分散行列表・プール後分散共分散行列表の作成、逆行列の算出というプロセスを経て、最後に判別係数と定数項を算出することで、線形判別関係式が完成します。
（例：不整脈症状=0.289×喫煙本数+0.210×飲酒日数－7.6）

各々の群の重心までの距離（マハラノビス汎距離）によって判別します。
Excelで行う場合、「分散共分散行列」から逆行列を算出し、平均との差分と掛け合わせて算出します。

マーケティング分野では主に、顧客のカテゴリー分類で最も効果を発揮しており、特に見込み顧客の分類、現在の顧客の分類では不可欠な分析です。また、金融機関における与信で重宝されています。

【参考文献】

『例題とExcel演習で学ぶ多変量解析回帰分析 回帰分析・判別分析・コンジョイント分析編』（菅民郎著、オーム社、2016年11月）